2021-2022學(xué)年浙江省衢溫“5+1”聯(lián)盟高二（上）期末數(shù)學(xué)試卷

一、選擇題：本大題共8小題，每小題5分，共40分．在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的.；

• 1．設(shè)集合A={x|-1＜x＜4}，B={2，3，4，5}，則A∩B=（　　）

  A．{2}

  B．{2，3}

  C．{3，4}

  D．{2，3，4}
  組卷：74引用：5難度：0.9

  解析

• 2．直線

  3

  x-y+1=0的傾斜角為（　　）

  A． π 6

  B． π 4

  C． π 3

  D． 2 π 3
  組卷：509引用：12難度：0.9

  解析

• 3．若tanθ=-2，則

  sinθ

  +

  3

  cosθ

  sinθ

  +

  cosθ

  =（　　）

  A．-2

  B．-1

  C．1

  D．2
  組卷：447引用：2難度：0.8

  解析

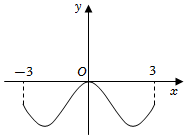• 4．已知函數(shù)f（x）的圖象如圖所示，則導(dǎo)函數(shù)f′（x）的圖象可能是（　　）

  A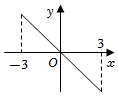．	B．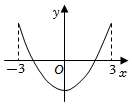
  C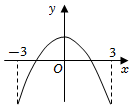．	D．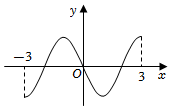
  組卷：701引用：7難度：0.7

  解析

• 5．已知圓

  C

  1

  ：

  （

  x

  -

  3

  ）

  2

  +

  （

  y

  -

  1

  ）

  2

  =

  a

  ，圓C₂：x²+y²-

  4

  3

  x-4y+7=0，則“a=1”是“兩圓內(nèi)切”的（　　）

  A．充分必要條件	B．充分不必要條件
  C．必要不充分條件	D．既不充分也不必要條件
  組卷：184引用：1難度：0.7

  解析

• 6．已知等差數(shù)列{a_n}的前n項(xiàng)和為S_n，首項(xiàng)a₁=1，若?n∈N^*，S₅≥S_n，則公差d的取值范圍為（　　）

  A． [ - 1 4 ，- 1 5 ]

  B． [ - 1 3 ，- 1 4 ]

  C． [ - 1 4 ，- 1 5 ）

  D． （ - 1 3 ，- 1 4 ]
  組卷：117引用：1難度：0.8

  解析

• 7．已知矩形ABCD，AB=1，BC=

  3

  ，沿對角線AC將△ABC折起，若二面角B-AC-D的余弦值為

  -

  1

  3

  ，則B與D之間距離為（　　）

  A．1

  B． 2

  C． 3

  D． 10 2
  組卷：901引用：11難度：0.5

  解析

四、解答題：本大題共6小題，共70分．解答應(yīng)寫出文字說明、證明過程或演算步驟.

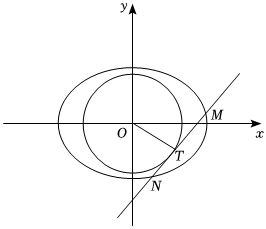• 21．已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  ，右焦點(diǎn)為F（

  2

  ，0），且離心率為

  2

  2

  ．
  （Ⅰ）求橢圓C的標(biāo)準(zhǔn)方程；
  （Ⅱ）設(shè)M，N是橢圓C上不同的兩點(diǎn)，且直線MN與圓O：

  x

  2

  +

  y

  2

  =

  4

  3

  相切，若T為弦MN的中點(diǎn)，求|OT|?|MN|的取值范圍．
  組卷：185引用：1難度：0.3

  解析

• 22．已知函數(shù)

  f

  （

  x

  ）

  =

  2

  lnx

  +

  a

  x

  -

  x

  ，且a＞0．
  （Ⅰ）當(dāng)a=1時(shí)，求函數(shù)f（x）的單調(diào)區(qū)間；
  （Ⅱ）記函數(shù)g（x）=f（x）+x,若函數(shù)g（x）有兩個(gè)零點(diǎn)x₁，x₂．
  （ⅰ）求實(shí)數(shù)a的取值范圍；
  （ⅱ）證明：

  x

  1

  +

  x

  2

  ＜

  2

  1

  -

  a

  ．
  組卷：175引用：1難度：0.3

  解析