2022-2023學年山東省菏澤市高二(上)期末數學試卷
發布:2024/4/20 14:35:0
一、選擇題(共8小題,每小題5分,滿分40分)
-
1.點A(-3,4,5)關于坐標平面Oxy對稱的點的坐標是( )
A.(3,4,5) B.(-3,-4,5) C.(-3,4,-5) D.(-3,-4,-5) 組卷:118引用:5難度:0.9 -
2.已知直線(m+1)x+3y+1=0與直線4x+my+1=0平行,則m的值為( )
A.3 B.-4 C.3或-4 D.3或4 組卷:506引用:8難度:0.8 -
3.已知直線l1:
x-y-1=0,若直線l2與l1垂直,則l2的傾斜角為( )3A.30° B.60° C.120° D.150° 組卷:253引用:6難度:0.8 -
4.在等比數列{an}中,
,a1=2,則公比q的值為( )S3=32A.1 B.-2 C.1或2 D.1或-2 組卷:230引用:2難度:0.8 -
5.已知等差數列{an}滿足a1=1,a5=9,若數列
的前n項和為Tn,則Tn=( ){1anan+1}A. n2n+1B. 2n2n+1C. 1n2D. 2n-12n+1組卷:200引用:3難度:0.6 -
6.已知圓C:x2+y2-6x=0與直線l:2x+y=1,則圓C上到直線l的距離為1的點的個數是( )
A.1 B.2 C.3 D.4 組卷:247引用:4難度:0.8 -
7.雙曲線y=
的焦距為( )1xA. 2B.2 2C.2 D.4 組卷:29引用:3難度:0.9
四、解答題(共6小題,滿分70分)
-
21.已知雙曲線C:
-x2a2=1(a>0,b>0)的實軸長為2,且雙曲線C上任一點P到它的兩條漸近線的距離之積為y2b2.23
(1)求雙曲線C的標準方程;
(2)已知過點M(x0,y0)的直線l與雙曲線C交于AB兩點.
(i)當x0=1,y0=1時,M能否是線段AB的中點?若能,求出l的方程;若不能,說明理由;
(ii)若點M(x0,y0)不是線段AB的中點,寫出x0,y0所滿足的關系式(不要求證明).組卷:33引用:1難度:0.4 -
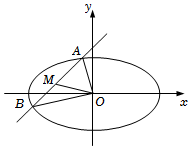 22.已知橢圓的離心率是C:x2a2+y2b2=1(a>b>0),且過點P(2,1).32
22.已知橢圓的離心率是C:x2a2+y2b2=1(a>b>0),且過點P(2,1).32
(Ⅰ)求橢圓C的標準方程;
(Ⅱ)若直線l與橢圓C交于A、B兩點,線段AB的中點為M,O為坐標原點,且,求△AOB面積的最大值.|OM|=2組卷:332引用:6難度:0.5


