2016-2017學年江西省新余一中高三（上）開學數學試卷（文科）

一、選擇題：本大題共12個小題，每小題5分，共60分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．設A、B是非空集合，定義A⊙B={x|x∈A，且x?B}，已知A={x|x²-x-2≤0}，B={x|y=

  1

  1

  -

  x

  }，則A⊙B=（　　）

  A．?

  B．[-1，2]

  C．[1，2]

  D．（1，2]
  組卷：14引用：2難度：0.9

  解析

• 2．已知i是虛數單位，復數z=

  1

  a

  -

  i

  （a∈R）在復平面內對應的點位于直線y=2x上，則a=（　　）

  A．2

  B． 1 2

  C．-2

  D．- 1 2
  組卷：10引用：3難度：0.9

  解析

• 3．已知定義域為[a-4，2a-2]的奇函數f（x）=2016x³-sinx+b+2，則f（a）+f（b）的值為（　　）

  A．0

  B．1

  C．2

  D．不能確定
  組卷：46引用：5難度：0.9

  解析

• 4．已知等比數列{a_n}中，a₂=2，a₆=8，則a₃a₄a₅=（　　）

  A．±64

  B．64

  C．32

  D．16
  組卷：105引用：6難度：0.9

  解析

• 5．已知m,n是兩條直線，α，β是兩個平面，則下列命題中不正確的是（　　）

  A．若m⊥β，m?α，則α⊥β	B．若m⊥α，α∥β，n?β，則m⊥n
  C．若α∥β，n⊥α，m⊥β，則m∥n	D．若m∥n,n∥α，α∥β，則m∥β
  組卷：18引用：2難度：0.7

  解析

• 6．已知圓C：x²+y²-2x=0，在圓C中任取一點P，則點P的橫坐標小于1的概率為（　　）

  A． 1 4

  B． 1 2

  C． 2 π

  D．以上都不對
  組卷：98引用：6難度：0.5

  解析

• 7．已知中心在原點且關于坐標軸對稱的雙曲線M的離心率為

  3

  ，且它的一個焦點到一條漸近線的距離為2，則雙曲線M的方程不可能是（　　）

  A． x 2 2 - y 2 4 =1

  B． y 2 2 - x 2 4 =1

  C．2x2-y2=4

  D． x 2 4 - y 2 2 =1
  組卷：10引用：2難度：0.7

  解析

• 8．執行如圖所示的程序框圖，若輸出的s=86，則判斷框內的正整數n的所有可能的值為（　　）
  

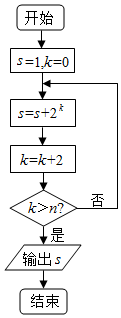
  A．7

  B．6，7

  C．6，7，8

  D．8，9
  組卷：16引用：4難度：0.9

  解析

[選修4-4：坐標系與參數方程]

• 23．以平面直角坐標系xOy的原點為極點，x軸的正半軸為極軸，建立極坐標系，兩種坐標系中取相同的長度單位，直線l的參數方程為

  x = 2 + 2 2 t

  y = 1 + 2 2 t

  ，圓C的極坐標方程為ρ=4

  2

  sin（θ+

  π

  4

  ）．
  （1）求直線l的普通方程與圓C的直角坐標系；
  （2）設曲線C與直線l交于A、B兩點，若P點的直角坐標為（2，1），求||PA|-|PB||的值．
  組卷：133引用：12難度：0.5

  解析

[選修4-5：不等式選講]

• 24．已知函數f（x）=|x-1|+|x-2|，記f（x）的最小值為k.
  （1）解不等式f（x）≤x+1；
  （2）是否存在正數a、b,同時滿足：2a+b=k,

  1

  a

  +

  2

  b

  =4？并證明．
  組卷：105引用：9難度：0.3

  解析