2023-2024學年黑龍江省哈爾濱實驗中學高二（上）開學數學試卷

一、單項選擇題（共8小題，每小題4分，共32分，在每小題給出的四個選項中，只有一項符合要求）

• 1．已知m、n是兩條不同直線，α、β是兩個不同平面，下列命題中正確的是（　　）

  A．若m∥α，n∥α，則m∥n

  B．若α∩β=n,m∥n,則m∥α且m∥β

  C．若α∥β，m∥α，n∥β，則m∥n

  D．若m∥α，m⊥β，則α⊥β
  組卷：45引用：3難度：0.7

  解析

• 2．在△ABC中，角A，B，C的對邊分別為a,b,c,若△ABC的面積

  S

  =

  -

  138

  2

  cos

  C

  ，且

  a

  =

  2

  ，

  b

  =

  3

  ，則c=（　　）

  A．2

  B． 5

  C． 6

  D． 7
  組卷：25引用：1難度：0.6

  解析

• 3．已知△ABC外接圓的圓心為O，且

  |

  AB

  +

  AC

  |

  =

  |

  AB

  -

  AC

  |

  ，

  |

  OA

  |

  =

  |

  AB

  |

  =

  1

  ，

  e

  是與

  BC

  方向相同的單位向量，則

  BA

  在

  BC

  上的投影向量為（　　）

  A． 1 2 e

  B． e

  C． 1 3 e

  D． - 1 2 e
  組卷：22引用：2難度：0.7

  解析

• 4．如圖，某同學為測量鸛雀樓的高度MN，在鸛雀樓的正東方向找到一座建筑物AB，高約為37m,在地面上點C處（B，C，N三點共線）測得建筑物頂部A，鸛雀樓頂部M的仰角分別為30°和45°，在A處測得樓頂部M的仰角為15°，則鸛雀樓的高度約為（　　）
  

  A．91m

  B．74m

  C．64m

  D．52m
  組卷：144引用：9難度：0.5

  解析

• 5．已知向量

  OA

  =

  （

  1

  ，

  1

  ）

  ，將向量

  OA

  繞原點O逆時針旋轉90°得到向量

  OB

  ，將向量

  OA

  繞原點O順時針旋轉135°得到向量

  OC

  ，則下列選項錯誤的是（　　）

  A． OA + OB + OC = 0

  B． | BC | = | CA |

  C． OA ? OB = 0

  D． CA ? AB = - 2
  組卷：20引用：3難度：0.7

  解析

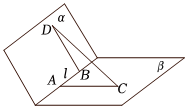• 6．如圖，二面角α-l-β等于120°，A、B是棱l上兩點，BD、AC分別在半平面α、β內，AC⊥l,BD⊥l,且AB=AC=BD=2，則CD的長等于（　　）

  A． 2 3

  B． 2 2

  C．4

  D．2
  組卷：658引用：33難度：0.5

  解析

四、解答題（共3小題，每小題12分，共36分）

• 18．在△ABC中，角A，B，C所對的邊分別為a,b,c,且a,b,c滿足

  b

  2

  +

  ac

  ac

  =

  sin

  A

  sin

  C

  +

  sin

  C

  sin

  A

  ，c=12．
  （1）已知D為線段BC上一點，且滿足AD=BD，若AC=

  189

  ，求CD的長；
  （2）若△ABC為銳角三角形，求△ABC面積的范圍．
  組卷：66引用：1難度：0.5

  解析

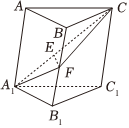• 19．如圖，在三棱柱ABC-A₁B₁C₁中，

  AC

  =

  2

  ，AB=1，E，F分別為A₁C，BB₁的中點，且EF⊥平面AA₁C₁C．
  （1）求棱BC的長度；
  （2）若BB₁⊥A₁B₁，且△A₁FC的面積

  S

  Δ

  A

  1

  FC

  =

  2

  2

  ，求二面角B₁-A₁F-C的正弦值．
  組卷：218引用：6難度：0.5

  解析