2022-2023學年山東省日照市嵐山區八年級（下）期中數學試卷

一、單選題（共0分）

• 1．如圖，在△ABC中，點D，E分別是AC，BC的中點，以點A為圓心，AD為半徑作圓弧交AB于點F．若AD=7，DE=5，則BF的長為（　　）

  A．2

  B．2.5

  C．3

  D．3.5
  組卷：1030引用：13難度：0.5

  解析

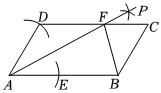• 2．如圖，在平行四邊形ABCD中，以點A為圓心，AD長為半徑作弧交AB于點E，再分別以點D，E為圓心，大于

  1

  2

  DE的長為半徑作弧，兩弧交于點P，作射線AP交CD于點F若AB=8，BF=5，則△BCF的周長為（　　）

  A．11

  B．12

  C．13

  D．14
  組卷：370引用：8難度：0.6

  解析

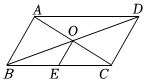• 3．已知四邊形ABCD是平行四邊形，對角線AC、BD交于點O，E是BC的中點，以下說法錯誤的是（　　）

  A．2OE=DC

  B．OA=OC

  C．∠BOE=∠OBA

  D．∠OBE=∠OCE
  組卷：144引用：5難度：0.7

  解析

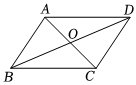• 4．如圖，平行四邊形ABCD的對角線AC，BD相交于點O，若AC=4，BD=6，則AB的長可能是（　　）

  A．7

  B．6

  C．5

  D．4
  組卷：1657引用：7難度：0.6

  解析

• 5．下列條件中，不能判別四邊形ABCD是平行四邊形的是（　　）

  A．AB∥CD，AB=CD	B．∠A=∠C，∠B=∠D
  C．AB=CD，AD=BC	D．AB=AD，BC=CD
  組卷：145引用：14難度：0.9

  解析

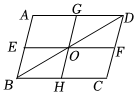• 6．如圖，在平行四邊形ABCD中，EF∥BC，GH∥AB，EF、GH的交點O在BD上，則圖中面積相等的平行四邊形有（　　）

  A．1對

  B．2對

  C．3對

  D．4對
  組卷：292引用：5難度：0.5

  解析

三、解答題

• 19．已知

  a

  =

  2

  -

  1

  ，

  b

  =

  2

  +

  1

  ，求下列各式的值．
  （1）a+b,ab；
  （2）

  a

  b

  -

  b

  a

  ．
  組卷：176引用：4難度：0.6

  解析

• 20．如圖1是著名的趙爽弦圖，由四個全等的直角三角形拼成，用它可以證明勾股定理，思路是：大正方形的面積有兩種求法，一種是等于c²，另一種是等于四個直角三角形與一個小正方形的面積之和，即

  1

  2

  ab

  ×

  4

  +

  （

  b

  -

  a

  ）

  2

  ，從而得到等式c²=

  1

  2

  ab

  ×

  4

  +

  （

  b

  -

  a

  ）

  2

  ，化簡便得結論a²+b²=c²．這里用兩種求法來表示同一個量從而得到等式或方程的方法，我們稱之為“雙求法”．現在，請你用“雙求法”解決下面兩個問題
  （1）如圖2，在Rt△ABC中，∠ACB=90°，CD是AB邊上的高，AC=3，BC=4，求CD的長度．
  （2）如圖3，在△ABC中，AD是BC邊上的高，AB=4，AC=5，BC=6，設BD=x,求x的值．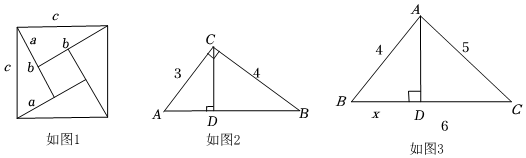
  組卷：1800引用：11難度：0.5

  解析