2022-2023學(xué)年廣東省東莞市虎門(mén)成才實(shí)驗(yàn)學(xué)校八年級(jí)（下）期中數(shù)學(xué)試卷

一、選擇題（本大題10小題，每小題3分，共30分）

• 1．下列各式是最簡(jiǎn)二次根式的是（　　）

  A． 13

  B． 12

  C． a 2

  D． 5 3
  組卷：1254引用：28難度：0.8

  解析

• 2．下列各組數(shù)據(jù)中，不能作為直角三角形的三邊長(zhǎng)的是（　　）

  A．3，4，5

  B．9，12，15

  C．1， 3 ，2

  D．5，12，14
  組卷：56引用：4難度：0.6

  解析

• 3．下列計(jì)算正確的是（　　）

  A． 2 × 1 2 =1

  B． 4 - 3 =1

  C． 6 ÷ 3 =2

  D． 8 =±2 2
  組卷：182引用：8難度：0.9

  解析

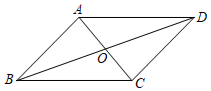• 4．如圖，?ABCD的對(duì)角線AC，BD相交于點(diǎn)O，則下列結(jié)論一定正確的是（　　）

  A．OB=OD

  B．AB=BC

  C．AC⊥BD

  D．∠ABD=∠CBD
  組卷：1292引用：21難度：0.6

  解析

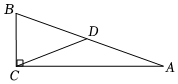• 5．如圖，在Rt△ABC中，CD是斜邊AB上的中線，∠A=20°，則∠BCD的度數(shù)是（　　）

  A．40°

  B．50°

  C．60°

  D．70°
  組卷：1174引用：15難度：0.8

  解析

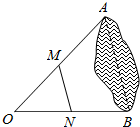• 6．如圖，為估計(jì)池塘岸邊A，B兩點(diǎn)間的距離，在池塘的一側(cè)選取點(diǎn)O，分別取OA，OB 的中點(diǎn)M，N，測(cè)得MN=32m,則A，B兩點(diǎn)間的距離是（　　）

  A．64m

  B．16m

  C．32m

  D．24m
  組卷：104引用：2難度：0.9

  解析

• 7．在四邊形ABCD中，AB=BC=CD=DA，如果添加一個(gè)條件，即可推出該四邊形是正方形，那么這個(gè)條件可以是（　　）

  A．AC⊥BD

  B．AB∥CD

  C．∠A=90°

  D．∠A=∠C
  組卷：503引用：5難度：0.9

  解析

五、解答題（三）（本大題2小題，每小題12分，共24分）

• 22．先閱讀下列材料，再解決問(wèn)題：
  閱讀材料：數(shù)學(xué)上有一種根號(hào)內(nèi)又帶根號(hào)的數(shù)，它們能通過(guò)完全平方公式a²±2ab+b²=（a±b）²及二次根式的性質(zhì)

  a

  2

  =|a|化去一層根號(hào)．例如：
  

  3

  +

  2

  2

  =

  3

  +

  2

  ×

  1

  ×

  2

  =

  1

  2

  +

  （

  2

  ）

  2

  +

  2

  ×

  1

  ×

  2

  =

  |

  1

  +

  2

  |

  =

  1

  +

  2

  ．
  解決問(wèn)題：
  （1）在括號(hào)內(nèi)填上適當(dāng)?shù)臄?shù)：
  

  4

  +

  2

  3

  =

  4

  +

  2

  ×

  1

  ×

  3

  =

  （

  ??

  ）

  2

  +

  （

  ??

  ）

  2

  +

  2

  ×

  1

  ×

  3

  =

  （

  ??

  ）

  2

  =|

  |=

  ．
  （2）根據(jù)上述思路，試將

  9

  -

  4

  5

  予以化簡(jiǎn)．
  組卷：184引用：1難度：0.7

  解析

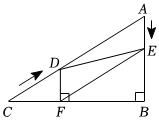• 23．如圖，在Rt△ABC中，∠B=90°，AC=60cm,∠A=60°，點(diǎn)D從點(diǎn)C出發(fā)沿CA方向以4cm/s的速度向點(diǎn)A勻速運(yùn)動(dòng)，同時(shí)點(diǎn)E從點(diǎn)A出發(fā)沿AB方向以2cm/s的速度向點(diǎn)B勻速運(yùn)動(dòng)，當(dāng)其中一個(gè)點(diǎn)到達(dá)終點(diǎn)時(shí)，另一個(gè)點(diǎn)也隨之停止運(yùn)動(dòng)．設(shè)點(diǎn)D，E運(yùn)動(dòng)的時(shí)間是t s（0＜t＜15）．DF⊥BC于點(diǎn)F，連接DE，EF．
  （1）填空：當(dāng)t=1時(shí)，CD=

  cm,AE=

  cm；
  （2）求證：四邊形AEFD是平行四邊形；
  （3）當(dāng)t為何值時(shí)，△DEF為直角三角形？
  組卷：58引用：1難度：0.6

  解析