當前位置：試卷中心 > 試卷詳情

2022-2023學年江西省宜春市宜豐中學高一（上）第三次月考數(shù)學試卷（12月份）

發(fā)布：2024/8/11 1:0:1

一、單選題（40分）

1．復數(shù)z=1+2i的虛部是（　　）
A．-2i B．2i C．-2 D．2
組卷：65引用：4難度：0.9
解析
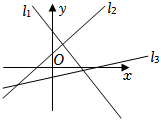2．如圖，直線l₁，l₂，l₃的斜率分別為k₁，k₂，k₃，則（　　）
A．k₁＜k₂＜k₃ B．k₃＜k₁＜k₂ C．k₃＜k₂＜k₁ D．k₁＜k₃＜k₂
組卷：58引用：6難度：0.8
解析
3．已知直線l₁：（k-3）x+（4-k）y+1=0與l₂：2（k-3）x-2y+3=0平行，則k的值是（　　）
A．1或3 B．5 C．3或5 D．2
組卷：124引用：4難度：0.9
解析
4．如圖，在三棱柱ABC-A₁B₁C₁中，AA₁⊥平面ABC，∠ACB=90°，
BC
=
A
A
1
=
3
，AC=1，則異面直線AC₁與CB₁所成角的余弦值為（　　）
A．
2
3
B．
6
4
C．
3
2
D．
2
5
5
組卷：71引用：5難度：0.6
解析
5．經(jīng)過點P（0，-1）作直線l,若直線l與連接A（1，-2），B（2，1）兩點的線段總有公共點，則直線l的傾斜角α的取值范圍是（　　）
A．
[
0
，
π
4
]
∪
[
3
π
4
，
π
）
B．
[
π
4
，
3
π
4
]
C．
[
π
4
，
π
2
）
∪
（
π
2
，
3
π
4
]
D．
（
0
，
π
4
）
∪
（
3
π
4
，
π
）
組卷：134引用：4難度：0.8
解析
6．在△ABC中，角A，B，C所對的邊分別是a,b,c,若b²+c²=a²-bc,則角A的大小為（　　）
A．
π
6
B．
π
3
C．
2
π
3
D．
5
π
6
組卷：15引用：1難度：0.9
解析
7．若
α
∈
（
π
2
，
π
）
，
cos
2
α
=
7
25
，則
sinα
sin
（
π
2
+
α
）
=（　　）
A．
-
3
4
B．
3
4
C．
4
3
D．
-
4
3
組卷：88引用：3難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內(nèi)容及下載

四、解答題（70分）

21．如圖，四棱柱ABCD-A₁B₁C₁D₁的底面ABCD為正方形，O為BD的中點，A₁O⊥底ABCD，AA₁=2AB=4．
（1）求證：平面A₁BD∥平面CD₁B₁；
（2）求直線A₁B與平面BDD₁B₁所成角的正弦值．
組卷：87引用：3難度：0.6
解析
22．美化環(huán)境，建設美好家園，大家一直在行動．現(xiàn)有一個直角三角形的綠地，∠C=90°，計劃在△MNC區(qū)域建設一個游樂場，其中AC=5米，BC=5
3
米，∠MCN=30°．
（1）若AM=4米，求△MNC的周長；
（2）設∠ACM=θ，求游樂場區(qū)域△MNC面積的最小值，并求出此時θ的值．
組卷：547引用：3難度：0.3
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業(yè) 發(fā)布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A． [ 0 ， π 4 ] ∪ [ 3 π 4 ， π ）	B． [ π 4 ， 3 π 4 ]
C． [ π 4 ， π 2 ） ∪ （ π 2 ， 3 π 4 ]	D．（ 0 ， π 4 ） ∪ （ 3 π 4 ， π ）

2022-2023學年江西省宜春市宜豐中學高一（上）第三次月考數(shù)學試卷（12月份）

一、單選題（40分）

1．復數(shù)z=1+2i的虛部是（ ）

2．如圖，直線l1，l2，l3的斜率分別為k1，k2，k3，則（ ）

3．已知直線l1：（k-3）x+（4-k）y+1=0與l2：2（k-3）x-2y+3=0平行，則k的值是（ ）

4．如圖，在三棱柱ABC-A1B1C1中，AA1⊥平面ABC，∠ACB=90°，BC=AA1=3，AC=1，則異面直線AC1與CB1所成角的余弦值為（ ）

5．經(jīng)過點P（0，-1）作直線l,若直線l與連接A（1，-2），B（2，1）兩點的線段總有公共點，則直線l的傾斜角α的取值范圍是（ ）

6．在△ABC中，角A，B，C所對的邊分別是a,b,c,若b2+c2=a2-bc,則角A的大小為（ ）

7．若α∈（π2，π），cos2α=725，則sinαsin（π2+α）=（ ）

四、解答題（70分）

21．如圖，四棱柱ABCD-A1B1C1D1的底面ABCD為正方形，O為BD的中點，A1O⊥底ABCD，AA1=2AB=4．（1）求證：平面A1BD∥平面CD1B1；（2）求直線A1B與平面BDD1B1所成角的正弦值．

1．復數(shù)z=1+2i的虛部是（　　）

2．如圖，直線l₁，l₂，l₃的斜率分別為k₁，k₂，k₃，則（　　）

3．已知直線l₁：（k-3）x+（4-k）y+1=0與l₂：2（k-3）x-2y+3=0平行，則k的值是（　　）

4．如圖，在三棱柱ABC-A₁B₁C₁中，AA₁⊥平面ABC，∠ACB=90°，
BC
=
A
A
1
=
3
，AC=1，則異面直線AC₁與CB₁所成角的余弦值為（　　）

5．經(jīng)過點P（0，-1）作直線l,若直線l與連接A（1，-2），B（2，1）兩點的線段總有公共點，則直線l的傾斜角α的取值范圍是（　　）

6．在△ABC中，角A，B，C所對的邊分別是a,b,c,若b²+c²=a²-bc,則角A的大小為（　　）

7．若
α
∈
（
π
2
，
π
）
，
cos
2
α
=
7
25
，則
sinα
sin
（
π
2
+
α
）
=（　　）

21．如圖，四棱柱ABCD-A₁B₁C₁D₁的底面ABCD為正方形，O為BD的中點，A₁O⊥底ABCD，AA₁=2AB=4．
（1）求證：平面A₁BD∥平面CD₁B₁；
（2）求直線A₁B與平面BDD₁B₁所成角的正弦值．