當(dāng)前位置：試卷中心 > 試卷詳情

2022-2023學(xué)年廣東省廣州中學(xué)高一（下）期中數(shù)學(xué)試卷

發(fā)布：2024/11/18 3:30:2

一、單選題（本題共8小題，每小題5分，共40分）

1．設(shè)D是△ABC所在平面內(nèi)一點(diǎn)，
BC
=
3
CD
，則
AD
=（　　）
A．
4
3
AB
+
1
3
AC
B．
4
3
AB
-
1
3
AC
C．
1
3
AB
-
4
3
AC
D．
-
1
3
AB
+
4
3
AC
組卷：101引用：2難度：0.7
解析
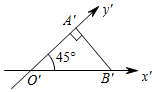2．如圖，已知等腰三角形O'A'B'是一個(gè)平面圖形的直觀圖，O'A'=A'B'，斜邊O'B'=2，則這個(gè)平面圖形的面積是（　　）
A．
2
2
B．1 C．
2
D．
2
2
組卷：688引用：24難度：0.5
解析
3．已知向量
a
=（m-1，1），
b
=（m,-2），則“m=2”是“
a
⊥
b
”的（　　）
A．充分不必要條件 B．必要不充分條件
C．充要條件 D．既不充分也不必要條件
組卷：825引用：12難度：0.9
解析
4．如圖，在正四面體ABCD中（棱長(zhǎng)均相等的四面體叫做正四面體），M是線段BC的中點(diǎn)，P是線段AM上的動(dòng)點(diǎn)，則直線DP和BC所成角的大小（　　）
A．90^o B．60^o
C．45^o D．與P的位置有關(guān)
組卷：361引用：5難度：0.8
解析
5．唐朝的狩獵景象浮雕銀杯如圖1所示，其浮雕臨摹了國畫、漆繪和墓室壁畫，體現(xiàn)了古人的智慧與工藝．它的盛酒部分可以近似地看作是半球與圓柱的組合體（假設(shè)內(nèi)壁表面光滑，忽略杯壁厚度），如圖2所示．已知球的半徑為R，酒杯的容積
11
3
π
R
3
，則其內(nèi)壁表面積為（　　）
A．12πR² B．10πR² C．8πR² D．6πR²
組卷：180引用：5難度：0.7
解析
6．在△ABC中，若A=60°，a=
3
，則
a
+
b
-
c
sin
A
+
sin
B
-
sin
C
=（　　）
A．
3
B．
3
2
C．2 D．
1
2
組卷：195引用：2難度：0.7
解析
7．已知四邊形ABCD是圓內(nèi)接四邊形，AB=4，AD=5，BD=3，則ABCD的周長(zhǎng)取最大值時(shí)，四邊形ABCD的面積為（　　）
A．
27
4
B．
51
4
C．
9
+
3
10
D．
3
+
3
10
組卷：199引用：4難度：0.6
解析

當(dāng)前模式為游客模式，立即登錄查看試卷全部?jī)?nèi)容及下載

四、解答題（本題共7小題，共70分．解答應(yīng)寫出文字說明、證明過程成演算步驟）

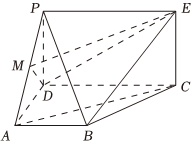22．如圖，PDCE為矩形，ABCD為梯形，平面PDCE⊥平面ABCD，∠BAD=∠ADC=90°，
AB
=
AD
=
1
2
CD
=
a
，
PD
=
2
a
．
（1）若M為PA中點(diǎn)，求證：AC∥平面MDE；
（2）求直線PB與直線CD所成角的大小；
（3）設(shè)平面PAD∩平面EBC=l,試判斷l(xiāng)與平面ABCD能否垂直？并求平面PAD與平面EBC所成銳二面角的大小．
組卷：116引用：3難度：0.3
解析
23．在△ABC中，內(nèi)角A，B，C對(duì)邊的邊長(zhǎng)分別是a,b,c,已知a²+c²=2b²．
（Ⅰ）若
B
=
π
4
，且A為鈍角，求內(nèi)角A與C的大小；
（Ⅱ）若b=2，求△ABC面積的最大值．
組卷：906引用：3難度：0.7
解析

0/60 進(jìn)入組卷

0/20 進(jìn)入試卷籃

布置作業(yè) 發(fā)布測(cè)評(píng) 反向細(xì)目表 平行組卷 下載答題卡 試卷分析 在線訓(xùn)練 收藏試卷

充值會(huì)員，資源免費(fèi)下載

A．充分不必要條件	B．必要不充分條件
C．充要條件	D．既不充分也不必要條件

A．90^o	B．60^o
C．45^o	D．與P的位置有關(guān)

2022-2023學(xué)年廣東省廣州中學(xué)高一（下）期中數(shù)學(xué)試卷

一、單選題（本題共8小題，每小題5分，共40分）

1．設(shè)D是△ABC所在平面內(nèi)一點(diǎn)，BC=3CD，則AD=（ ）

2．如圖，已知等腰三角形O'A'B'是一個(gè)平面圖形的直觀圖，O'A'=A'B'，斜邊O'B'=2，則這個(gè)平面圖形的面積是（ ）

3．已知向量a=（m-1，1），b=（m,-2），則“m=2”是“a⊥b”的（ ）

4．如圖，在正四面體ABCD中（棱長(zhǎng)均相等的四面體叫做正四面體），M是線段BC的中點(diǎn)，P是線段AM上的動(dòng)點(diǎn)，則直線DP和BC所成角的大小（ ）

6．在△ABC中，若A=60°，a=3，則a+b-csinA+sinB-sinC=（ ）

7．已知四邊形ABCD是圓內(nèi)接四邊形，AB=4，AD=5，BD=3，則ABCD的周長(zhǎng)取最大值時(shí)，四邊形ABCD的面積為（ ）

四、解答題（本題共7小題，共70分．解答應(yīng)寫出文字說明、證明過程成演算步驟）

23．在△ABC中，內(nèi)角A，B，C對(duì)邊的邊長(zhǎng)分別是a,b,c,已知a2+c2=2b2．（Ⅰ）若B=π4，且A為鈍角，求內(nèi)角A與C的大小；（Ⅱ）若b=2，求△ABC面積的最大值．

1．設(shè)D是△ABC所在平面內(nèi)一點(diǎn)，
BC
=
3
CD
，則
AD
=（　　）

2．如圖，已知等腰三角形O'A'B'是一個(gè)平面圖形的直觀圖，O'A'=A'B'，斜邊O'B'=2，則這個(gè)平面圖形的面積是（　　）

3．已知向量
a
=（m-1，1），
b
=（m,-2），則“m=2”是“
a
⊥
b
”的（　　）

4．如圖，在正四面體ABCD中（棱長(zhǎng)均相等的四面體叫做正四面體），M是線段BC的中點(diǎn)，P是線段AM上的動(dòng)點(diǎn)，則直線DP和BC所成角的大小（　　）

6．在△ABC中，若A=60°，a=
3
，則
a
+
b
-
c
sin
A
+
sin
B
-
sin
C
=（　　）

7．已知四邊形ABCD是圓內(nèi)接四邊形，AB=4，AD=5，BD=3，則ABCD的周長(zhǎng)取最大值時(shí)，四邊形ABCD的面積為（　　）

23．在△ABC中，內(nèi)角A，B，C對(duì)邊的邊長(zhǎng)分別是a,b,c,已知a²+c²=2b²．
（Ⅰ）若
B
=
π
4
，且A為鈍角，求內(nèi)角A與C的大小；
（Ⅱ）若b=2，求△ABC面積的最大值．