2022-2023學年江蘇省蘇州中學高一（下）月考數學試卷（3月份）

一、單項選擇題：本小題共8小題，每小題5分，共40分，在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知平面向量

  a

  =（2，4），

  b

  =（-3，m+2），

  a

  ∥

  b

  ，則m=（　　）

  A．-2

  B．-8

  C．6

  D．4
  組卷：96引用：2難度：0.8

  解析

• 2．《九章算術》是我國算術名著，其中有這樣一個問題：“今有宛田，下周三十步，徑十六步，問為田幾何？”意思是說：現有扇形田，弧長三十步，直徑十六步，問面積多少？書中給出計算方法，以徑乘周，四而一，即扇形的面積等于直徑乘以弧長再除以4，在此問題中，扇形的圓心角的弧度數是（　　）

  A． 4 15

  B． 15 4

  C． 15 8

  D．120
  組卷：700引用：10難度：0.8

  解析

• 3．已知函數f（x）=sinxcos（2x+φ）（φ∈[0，π]）為偶函數，則φ=（　　）

  A．0

  B． π 4

  C． π 2

  D．π
  組卷：372引用：3難度：0.8

  解析

• 4．已知

  a

  =

  （

  -

  2

  ，-

  1

  ）

  ，

  b

  =

  （

  λ

  ，

  1

  ）

  ，則λ＞-

  1

  2

  是“

  a

  與

  b

  的夾角為鈍角”的（　　）條件

  A．充分不必要	B．必要不充分
  C．充分必要	D．既不充分也不必要
  組卷：375引用：8難度：0.8

  解析

• 5．若點P（cosα，sinα）在直線y=-2x上，則sin²α+cos（2α+

  π

  2

  ）=（　　）

  A．0

  B． 2 5

  C． 6 5

  D． 8 5
  組卷：181引用：5難度：0.9

  解析

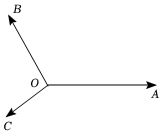• 6．如圖所示，平面內有三個向量

  OA

  ，

  OB

  ，

  OC

  ，

  OA

  與

  OB

  的夾角為120°，

  OA

  與

  OC

  的夾角為150°，且

  |

  OA

  |

  =

  |

  OB

  |

  =

  1

  ，

  |

  OC

  |

  =

  3

  3

  ，若

  OB

  =

  λ

  OA

  +

  μ

  OC

  （λ，μ∈R），則λ+μ=（　　）

  A．1

  B．-1

  C．-4

  D．-5
  組卷：92引用：5難度：0.6

  解析

• 7．已知f（x）=asin2x+bcos2x,其中a,b∈R，ab≠0，若f（x）＜|f（

  π

  6

  ）|對x∈R恒成立，且f（

  π

  2

  ）＞0，則f（x）的單調遞增區間是（　　）

  A．[kπ- π 3 ，kπ+ π 6 ]（k∈Z）	B．[kπ+ π 6 ，kπ+ 2 π 3 ]（k∈Z）
  C．[kπ，kπ+ π 2 ]（k∈Z）	D．[kπ- π 2 ，kπ]（k∈Z）
  組卷：141引用：2難度：0.6

  解析

四、解答題：本題共6小題，共70分，解答應寫出文字說明、證明過程或驗算步驟.

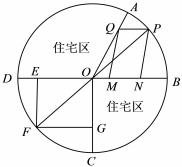• 21．如圖，某圓形小區有兩塊空余綠化扇形草地AOB（圓心角為

  π

  3

  ）和COD（圓心角為

  π

  2

  ），BD為圓的直徑．現分別要設計出兩塊社區活動區域，其中一塊為矩形區域OEFG，一塊為平行四邊形區域MNPQ，已知圓的直徑PF=2百米，且點P在劣弧AB上（不含端點），點Q在OA上、點G在OC上、點M和N在OB上、點E在OD上，記∠BOP=θ．
  （1）經設計，當

  OE

  -

  1

  2

  MN

  達到最大值時，取得最佳觀賞效果，求θ取何值時，

  OE

  -

  1

  2

  MN

  最大，最大值是多少？
  （2）設矩形OEFG和平行四邊形MNPQ面積和為S，求S的最大值及此時cos2θ的值．
  組卷：183引用：5難度：0.4

  解析

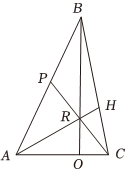• 22．在△ABC中，P為AB的中點，O在邊AC上，BO交CP于R，且|

  AO

  |=2|

  OC

  |，設

  AB

  =

  a

  ，

  AC

  =

  b

  ．
  （1）試用

  a

  ，

  b

  表示

  AR

  ；
  （2）若H在BC上，且RH⊥BC，設|

  a

  |=2，|

  b

  |=1，令∠BAC=θ，若θ∈[

  π

  3

  ，

  2

  π

  3

  ]，求

  |

  CH

  |

  |

  CB

  |

  的取值范圍．
  組卷：57引用：1難度：0.5

  解析