2023-2024學年北京交大附中高三（上）診斷數學試卷（10月份）

一、選擇題。（每小題4分，共40分）

• 1．已知全集U=R，集合A={x|-2≤x≤3}，B={x|x＜-1或x＞4}，那么集合A∩（?_UB）等于（　　）

  A．{x|-2≤x≤4}

  B．{x|x≤3或x≥4}

  C．{x|-2≤x＜-1}

  D．{x|-1≤x≤3}
  組卷：751引用：37難度：0.9

  解析

• 2．已知向量

  a

  =（m,2），

  b

  =（2，-1）．若

  a

  ∥

  b

  ，則m的值為（　　）

  A．4

  B．1

  C．-4

  D．-1
  組卷：252引用：7難度：0.9

  解析

• 3．命題p：?x＞2，x²-1＞0，則￢p是（　　）

  A．?x＞2，x2-1≤0	B．?x≤2，x2-1＞0
  C．?x＞2，x2-1≤0	D．?x≤2，x2-1≤0
  組卷：428引用：61難度：0.9

  解析

• 4．已知函數f（x）=lnx+x-4，在下列區間中，包含f（x）零點的區間是（　　）

  A．（0，1）

  B．（1，2）

  C．（2，3）

  D．（3，4）
  組卷：503引用：8難度：0.7

  解析

• 5．為了得到函數

  y

  =

  -

  sin

  （

  x

  -

  π

  3

  ）

  的圖象，只需把函數y=sinx的圖象上的所有點（　　）

  A．向左平移 2 π 3 個單位長度

  B．向左平移 π 3 個單位長度

  C．向右平移 π 3 個單位長度

  D．向右平移 5 π 3 個單位長度
  組卷：467引用：3難度：0.7

  解析

• 6．在△ABC中，

  B

  =

  π

  4

  ，

  AC

  =

  2

  ，則“

  BC

  =

  3

  ”是“

  A

  =

  π

  3

  ”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：101引用：1難度：0.6

  解析

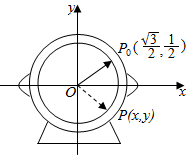• 7．如圖，為了研究鐘表與三角函數的關系，建立如圖所示的坐標系，設秒針尖位置p（x,y）．若初始位置為P₀（

  3

  2

  ，

  1

  2

  ），當秒針從P₀（注此時t=0）正常開始走時，那么點P的縱坐標y與時間t的函數關系為（　　）

  A．y=sin（ π 30 t + π 6 ）	B． y = sin （ - π 60 t - π 6 ）
  C．y=sin（- π 30 t + π 6 ）	D．y=sin（- π 30 t - π 3 ）
  組卷：1554引用：30難度：0.7

  解析

三、解答題。（共85分）

• 20．已知函數f（x）=

  1

  2

  x²-x+alnx,（a＞0）．
  （1）若a=1，求f（x）在（1，f（1））處的切線方程；
  （2）討論f（x）的單調性；
  （3）若f（x）存在兩個極值點x₁，x₂，求證：f（x₁）+f（x₂）＞

  -

  3

  -

  2

  ln

  2

  4

  ．
  組卷：1289引用：5難度：0.3

  解析

• 21．設集合S={a₁，a₂，…a_n}（n≥3），其中

  a

  i

  ∈

  N

  *

  ，i=1，2，…，n.若集合S滿足對于任意的兩個非空集合A，B?S，都有集合A的所有元素之和與集合B的元素之和不相等，則稱集合S具有性質P．
  （1）判斷集合{1，2，3，5，9}，{1，3，5，11}是否具有性質P，并說明理由；
  （2）若集合

  S

  =

  {

  a

  1

  ，

  a

  2

  ，

  ?

  ，

  a

  n

  }

  （

  n

  ∈

  N

  *

  ）

  具有性質P，求證：?k≤n,

  a

  1

  +

  a

  2

  +

  ?

  +

  a

  k

  ≥

  2

  k

  -

  1

  ，

  k

  ∈

  N

  *

  ；
  （3）若集合S={a₁，a₂，…，a₂₀₂₃}具有性質P，求

  1

  a

  1

  +

  1

  a

  2

  +

  ?

  +

  1

  a

  2023

  的最大值．
  組卷：58引用：1難度：0.5

  解析