當前位置：試卷中心 > 試卷詳情

2021-2022學年四川省成都市蓉城名校聯盟高二（上）入學數學試卷（理科）

發布：2024/12/21 20:30:2

1．若向量
a
=（2，-3），
b
=（-1，m），且
a
⊥
b
，則實數m的值為（　　）
A．-
3
2
B．-
2
3
C．
2
3
D．
3
2
組卷：50引用：2難度：0.7
解析
2．
（
cos
π
12
-
sin
π
12
）
（
cos
π
12
+
sin
π
12
）
=（　　）
A．
-
3
2
B．
-
1
2
C．
1
2
D．
3
2
組卷：803引用：36難度：0.9
解析
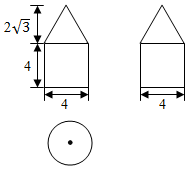3．如圖是由圓柱與圓錐組合而成的幾何體的三視圖，則該幾何體的表面積為（　　）
A．20π B．24π C．28π D．32π
組卷：7485引用：73難度：0.7
解析
4．已知數列{a_n}滿足a₁=3，a_n=1-
1
a
n
-
1
（n≥2），則a₁₁的值為（　　）
A．3 B．2 C．
2
3
D．-
1
2
組卷：168引用：2難度：0.7
解析
5．在△ABC中，BC=2，sinA=
3
3
，B=
π
3
，則AC的值為（　　）
A．
2
2
3
B．
4
3
C．3 D．3
2
組卷：196引用：2難度：0.9
解析
6．已知a,b,l表示不同的直線，α，β表示不同的平面，則下列說法正確的是（　　）
A．若a∥b,b?α，則a∥α
B．若α∥β，a?α，b?β，則a∥b
C．若l⊥a,l⊥b,a?α，b?α，則l⊥α
D．若α⊥β，α∩β=a,l?α，l⊥a,則l⊥β
組卷：50引用：6難度：0.7
解析
7．已知等差數列{a_n}中，a₃=-5，a₁₁=11，記數列{a_n}的前n項和為S_n，則S₁₃的值為（　　）
A．42 B．39 C．36 D．33
組卷：224引用：3難度：0.9
解析