2021-2022學年黑龍江省大慶五十六中高二（下）期中數學試卷

一、單選題

• 1．已知函數f（x）的定義域為R，若

  lim

  Δ

  x

  →

  0

  f

  （

  1

  +

  △

  x

  ）

  -

  f

  （

  1

  ）

  △

  x

  =

  1

  ，則f'（1）=（　　）

  A．1

  B．2

  C． 1 2

  D．4
  組卷：67引用：1難度：0.8

  解析

• 2．函數f（x）=2x-sinx在（-∞，+∞）上是（　　）

  A．增函數

  B．減函數

  C．先增后減

  D．不確定
  組卷：55引用：8難度：0.7

  解析

• 3．2022年北京冬奧會的順利召開，引起了大家對冰雪運動的關注．若A，B，C三人在自由式滑雪、花樣滑冰、冰壺和跳臺滑雪這四項運動中任選一項進行體驗，則不同的選法共有（　　）

  A．12種

  B．16種

  C．64種

  D．81種
  組卷：587引用：10難度：0.7

  解析

• 4．已知離散型隨機變量ξ的分布列如表所示，則表中p值等于（　　）
  

  ξ	0	1	2
  P	0.45	p	0.30

  A．0.50

  B．0.25

  C．0.20

  D．0.15
  組卷：60引用：1難度：0.9

  解析

• 5．袋中裝有大小相同的10個紅球，5個黑球，每次隨機取出1個球，若取得黑球，則另換1個紅球放入袋中，直到取到紅球為止，若抽取的次數為X，則表示“放入3個紅球”的事件為（　　）

  A．X=4

  B．X=5

  C．X=6

  D．X≤4
  組卷：20引用：4難度：0.7

  解析

• 6．函數y=f（x）的圖像如圖所示，則（　　）
  

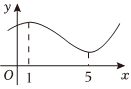
  A．f'（3）＞0	B．f'（3）＜0
  C．f'（3）=0	D．f'（3）的符號不確定
  組卷：21引用：2難度：0.7

  解析

• 7．下列說法不正確的是（　　）

  A．隨機變量的方差和標準差越小，則偏離變量的平均程度越小

  B．若a是常數，則D（a）=0

  C．離散型隨機變量的方差反映了隨機變量偏離于均值的平均程度

  D．離散型隨機變量的方差越大，隨機變量越穩定
  組卷：37引用：2難度：0.7

  解析

三、解答題

• 21．某校為緩解高三學生壓力，舉辦了一場趣味運動會，其中有一個項目為籃球定點投籃，比賽分為初賽和復賽．初賽規則為：每人最多投3次，每次投籃的結果相互獨立．在A處每投進一球得3分，在B處每投進一球得2分，否則得0分．將學生得分逐次累加并用X表示，如果X的值不低于3分就判定為通過初賽，立即停止投籃，否則應繼續投籃，直到投完三次為止．現有兩種投籃方案：
  方案1：先在A處投一球，以后都在B處投；
  方案2：都在B處投籃；
  已知甲同學在A處投籃的命中率為

  1

  4

  ，在B處投籃的命中率為

  4

  5

  ．
  （1）若甲同學選擇方案1，求他初賽結束后所得總分X的分布列和數學期望E（X）；
  （2）你認為甲同學選擇哪種方案通過初賽的可能性更大？說明理由．
  組卷：66引用：3難度：0.5

  解析

• 22．已知a∈R，函數

  f

  （

  x

  ）

  =

  2

  x

  +

  alnx

  （

  a

  ＞

  0

  ）

  ．
  （1）求函數f（x）的極值；
  （2）若函數f（x）＞0恒成立，求a的取值范圍．
  組卷：20引用：1難度：0.6

  解析