2023-2024學(xué)年遼寧省大連育明高級(jí)中學(xué)高二（上）期中數(shù)學(xué)試卷

一、單項(xiàng)選擇題：（本題共8小題，每小題5分，共：40分.在每個(gè)小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的.

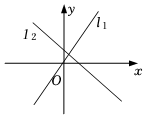• 1．如圖，記直線l₁，l₂的斜率分別為k₁，k₂，傾斜角分別為α₁，α₂則下列結(jié)論正確的是（　　）

  A．k1＞k2，α1＞α2	B．k1＞k2，α1＜α2
  C．k1＜k2，α1＞α2	D．k1＜k2，α1＜α2
  組卷：162引用：3難度：0.9

  解析

• 2．已知兩點(diǎn)A（1，3），B（4，2），直線l：kx+y-3k-1=0線段AB相交，則k的取值范圍是（　　）

  A．-1≤k≤1

  B．k≤-1或k≥1

  C．k≤1

  D．k≥-1
  組卷：198引用：5難度：0.7

  解析

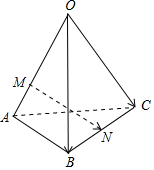• 3．如圖，空間四邊形OABC中，

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，點(diǎn)M在線段OA上，且OM=2MA，點(diǎn)N為BC的中點(diǎn)，則

  MN

  =（　　）

  A．- 2 3 a + 1 2 b + 1 2 c	B． 1 2 a - 2 3 b + 1 2 c
  C． 1 2 a + 1 2 b - 1 2 c	D． 2 3 a + 2 3 b - 1 2 c
  組卷：3582引用：38難度：0.9

  解析

• 4．已知點(diǎn)A（1，2）在圓C：x²+y²+mx-2y+2=0外，則實(shí)數(shù)m的取值范圍為（　　）

  A．（-3，-2）∪（2，+∞）	B．（-3，-2）∪（3，+∞）
  C．（-2，+∞）	D．（-3，+∞）
  組卷：1080引用：16難度：0.7

  解析

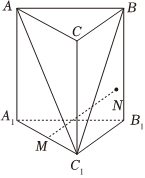• 5．如圖，在三棱柱ABC-A₁B₁C₁中，M為A₁C₁的中點(diǎn)，N為側(cè)面BCC₁B₁上的一點(diǎn)，且MN∥平面ABC₁，若點(diǎn)N的軌跡長度為2，則（　　）

  A．AC1=4

  B．BC1=4

  C．AB1=6

  D．B1C=6
  組卷：337引用：9難度：0.6

  解析

• 6．方程

  x

  2

  λ

  2

  -

  4

  +

  y

  2

  3

  -

  λ

  =

  1

  表示焦距為

  2

  5

  的雙曲線，則實(shí)數(shù)λ的值為（　　）

  A．1

  B．-4或1

  C．-2或-4

  D．-2或1
  組卷：345引用：2難度：0.7

  解析

• 7．已知拋物線C：y²=8x上的一點(diǎn)P，直線l₁：x=-2，l₂：3x-5y+30=0，則P到這兩條直線的距離之和的最小值為（　　）

  A．2

  B．2 34

  C． 16 15 34

  D． 18 17 34
  組卷：58引用：4難度：0.7

  解析

四、解答題：（本題共6小題，共計(jì)70分.解答時(shí)應(yīng)寫出文字說明、證明過程或演算步驟.）.

• 21．如圖，等腰直角△ACD的斜邊AC為直角△ABC的直角邊，E是AC的中點(diǎn)，F(xiàn)在BC上．將三角形ACD沿AC翻折，分別連接DE，DF，EF，使得平面DEF⊥平面ABC．已知AC=2，∠B=30°．
  
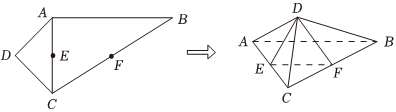
  （1）證明：EF∥平面ABD；
  （2）若DF=

  2

  ，求二面角A-BC-D的余弦值．
  組卷：114引用：3難度：0.6

  解析

• 22．在平面直角坐標(biāo)系中，A（-1，0），B（1，0），設(shè)△ABC的內(nèi)切圓分別與邊AC，BC，AB相切于點(diǎn)P，Q，R，已知|CP|=1，記動(dòng)點(diǎn)C的軌跡為曲線E．
  （1）求曲線E的方程；
  （2）過點(diǎn)B（1，0）作直線l交曲線E于M，N兩點(diǎn)，且點(diǎn)M位于x軸上方，已知A₁（-2，0），A₂（2，0）記直線A₁M，A₂N，A₁N的斜率分別為k₁，k₂，k₃．
  ①證明：k₁k₃，

  k

  1

  k

  2

  為定值；
  ②設(shè)點(diǎn)N關(guān)于x軸的對稱點(diǎn)為N₁，求△BMN₁面積的最大值．
  組卷：282引用：2難度：0.4

  解析