2022-2023學年湖北省武漢市七校高二（上）期中數學試卷

一、單項選擇題（本大題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.）

• 1．某校高一年級15個班參加合唱比賽，得分從小到大排序依次為：85，85，86，87，88，89，90，91，91，91，92，93，94，96，98，則這組數據的80%分位數是（　　）

  A．90

  B．93.5

  C．86

  D．93
  組卷：139引用：3難度：0.8

  解析

• 2．若m,n是兩條不同直線，α，β是兩個不同平面，則下列命題不正確的是（　　）

  A．若m⊥α，n∥α，則m⊥n	B．若α⊥β，m∥α，則m⊥β
  C．若m⊥α，m∥β，則α⊥β	D．若n⊥α，n∥m,則m⊥α
  組卷：21引用：4難度：0.7

  解析

• 3．在下列各事件中，發生的可能性最大的為（　　）

  A．任意買1張電影票，座位號是奇數

  B．擲1枚骰子，點數小于等于2

  C．有10000張彩票，其中100張是中獎彩票，從中隨機買1張是中獎彩票

  D．一袋中裝有8個紅球，2個白球，從中隨機摸出1個球是紅球
  組卷：307引用：5難度：0.9

  解析

• 4．“λ=3”是“直線（2λ-3）x+（λ+1）y+3=0與直線（λ+1）x-λy+3=0互相垂直”的（　　）

  A．充分不必要條件	B．充要條件
  C．必要不充分條件	D．既不充分也不必要條件
  組卷：338引用：9難度：0.8

  解析

• 5．若直線l：kx-y-2=0與曲線

  C

  ：

  1

  -

  （

  y

  -

  1

  ）

  2

  =

  x

  -

  1

  有兩個交點，則實數k的取值范圍是（　　）

  A． （ 4 3 ， 2 ]	B． （ 4 3 ， 4 ）
  C． [ - 2 ， 4 3 ） ∪ （ 4 3 ， 2 ]	D． （ 4 3 ， + ∞ ）
  組卷：487引用：36難度：0.6

  解析

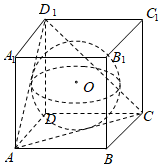• 6．如圖，已知球O是棱長為1的正方體ABCD-A₁B₁C₁D₁的內切球，則平面ACD₁截球O的截面面積為（　　）

  A． 6 6 π

  B． π 3

  C． π 6

  D． 3 3 π
  組卷：587引用：11難度：0.7

  解析

• 7．古希臘幾何學家阿波羅尼斯證明過這樣一個命題：平面內到兩定點距離之比為常數k（k＞0，k≠1）的點的軌跡是圓，后人將這個圓稱為阿波羅尼斯圓．若平面內兩定點A，B的距離為2，動點P滿足

  |

  PB

  |

  |

  PA

  |

  =

  3

  ，若點P不在直線AB上，則△PAB面積的最大值為（　　）

  A．1

  B． 3

  C．2

  D．2 3
  組卷：129引用：8難度：0.6

  解析

四、解答題（本大題共6大題，共70分.解答應寫出文字說明，證明過程或演算步驟.）

• 21．已知圓C：x²+y²+6x-6y+8=0，直線x-y+2=0是圓E與圓C的公共弦AB所在直線方程，且圓E的圓心在直線4x-y=0上．
  （1）求公共弦AB的長度；
  （2）求圓E的方程；
  （3）過點Q（-1，0）分別作直線MN，RS，交圓E于M，N，R，S四點，且MN⊥RS，求四邊形MRNS面積的最大值與最小值．
  組卷：95引用：2難度：0.5

  解析

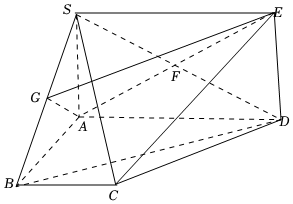• 22．如圖，已知SA垂直于梯形ABCD所在的平面，矩形SADE的對角線交于點F，G為SB的中點，

  ∠

  ABC

  =∠

  BAD

  =

  π

  2

  ，

  SA

  =

  AB

  =

  BC

  =

  1

  2

  AD

  =

  1

  ．
  （1）求證：BD∥平面AEG；
  （2）求二面角C-SD-E的余弦值；
  （3）在線段EG上是否存在一點H，使得BH與平面SCD所成角的大小為

  π

  6

  ？若存在，求出GH的長；若不存在，說明理由．
  組卷：266引用：8難度：0.4

  解析