2022-2023學年浙江大學附中高二（上）期中數學試卷

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．直線l：

  3

  x-3y+1=0的傾斜角為（　　）

  A． π 3

  B． π 4

  C． π 6

  D． π 2
  組卷：308引用：6難度：0.8

  解析

• 2．已知直線l的方向向量為

  m

  ，平面α的法向量為

  n

  ，則“

  m

  ?

  n

  =

  0

  ”是“l∥α”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：162引用：14難度：0.8

  解析

• 3．若直線l₁：2mx-y+1=0與l₂：（m-l）x+my+2=0互相垂直，則實數m=（　　）

  A． 2 3

  B．-1或0

  C． 3 2 或0

  D． 3 2
  組卷：105引用：3難度：0.7

  解析

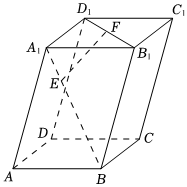• 4．如圖，在平行六面體ABCD-A₁B₁C₁D₁中，點E在面對角線A₁B上，滿足

  A

  1

  E

  =

  1

  3

  A

  1

  B

  ，點F為面對角線B₁D₁的中點，若

  A

  A

  1

  =

  a

  ，

  AB

  =

  b

  ，

  AD

  =

  c

  ，則

  EF

  =（　　）

  A． 1 3 a + 1 6 b + 1 2 c	B． 1 6 a + 1 3 b + 1 2 c
  C． 1 2 a + 1 3 b + 1 6 c	D． 1 6 a + 1 2 b + 1 3 c
  組卷：74引用：5難度：0.8

  解析

• 5．某學校高一年級、高二年級、高三年級的學生數量之比為2：m：1，為了解該校學生的住宿情況，現用比例分配的分層抽樣方法抽取一個容量為n的樣本，在樣本中，高二年級學生比高一年級多40位，比高三年級多80位，則n=（　　）

  A．240

  B．280

  C．320

  D．360
  組卷：71引用：3難度：0.8

  解析

• 6．已知x,y滿足x²+y²+2x-2y-3=0，若不等式2x+y-c＜0恒成立，則c的取值范圍是（　　）

  A．（-∞，-4）

  B．（4，+∞）

  C．（6，+∞）

  D．（-6，4）
  組卷：32引用：4難度：0.6

  解析

• 7．在平面直角坐標系中，O為坐標原點，A，B為平面上兩點，且

  OA

  ?

  OB

  =0，M為線段AB中點，其坐標為（a,b），若

  5

  |

  OM

  |

  =

  |

  2

  a

  +

  b

  -

  4

  |，則|OM|的最小值為（　　）

  A． 5 5

  B． 2 5 5

  C． 3 3

  D． 5
  組卷：21引用：4難度：0.6

  解析

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

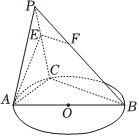• 21．如圖，C是以AB為直徑的圓O上異于A，B的點，平面PAC⊥平面ABC，△PAC為正三角形，E，F分別是棱PC，PB上的點，且滿足

  PE

  PC

  =

  PF

  PB

  =λ（0＜λ＜1）．
  （1）求證：BC⊥AE；
  （2）是否存在λ，使得直線AP與平面AEF所成角的正弦值為

  21

  14

  ？若存在，求出λ的值；若不存在，請說明理由．
  組卷：16引用：2難度：0.5

  解析

• 22．已知點E（4cosα，0），F（0，4sinα）（α∈R）為平面直角坐標系xOy中的點，點P為線段EF的中點，當α變化時，點P形成的軌跡π與x軸交于點A，B（A點在左側），與y軸正半軸交于點C．
  （1）求P點的軌跡π的方程；
  （2）設點M是軌跡π上任意一點（不在坐標軸上），直線CM交x軸于點D⊥，直線BM交直線AC于點N．
  ①若D點坐標為（2

  3

  ，0），求線段CM的長；
  ②求證：2k_ND-k_MB為定值．
  組卷：26引用：1難度：0.9

  解析