2022-2023學年浙江省寧波市余姚市高二（上）期末數學試卷

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．直線y=x+1的傾斜角為（　　）

  A．0

  B． π 4

  C． π 2

  D． 3 π 4
  組卷：35引用：1難度：0.7

  解析

• 2．已知

  a

  =

  （

  1

  ，

  2

  ，

  5

  ）

  ，

  b

  =

  （

  x

  -

  2

  ，

  1

  ，

  x

  ）

  ，若

  a

  ∥

  b

  ，則x=（　　）

  A．-2

  B． 1 2

  C． 5 2

  D． 7 2
  組卷：104引用：1難度：0.7

  解析

• 3．曲線f（x）=

  lnx

  x

  在點（1，f（1））處的切線方程為（　　）

  A．x+y=0

  B．x-y=0

  C．x+y-1=0

  D．x-y-1=0
  組卷：324引用：3難度：0.7

  解析

• 4．已知F是橢圓

  x

  2

  16

  +

  y

  2

  7

  =

  1

  的左焦點，P為橢圓上任意一點，點Q的坐標為（-2，1），則|PQ|+|PF|的最小值為（　　）

  A． 1 + 2

  B． 8 - 26

  C．3

  D． 2 + 5
  組卷：133引用：1難度：0.5

  解析

• 5．在四面體ABCD中，△ABC為正三角形，DB⊥平面ABC，且AB=BD，若

  3

  AE

  =

  AB

  ，

  2

  CF

  =

  CD

  ，則異面直線DE和BF所成角的余弦值等于（　　）

  A． 26 13

  B． - 26 13

  C． 2 39 39

  D． - 2 39 39
  組卷：64引用：1難度：0.6

  解析

• 6．某中學響應政府號召，積極推動“公益一小時”，鼓勵學生利用暑假時間積極參與社區服務，為了保障學生安全，與社區溝通實行點對點服務．原計劃第一批派遣18名學生，以后每批增加6人．由于志愿者人數暴漲，學校與社區臨時決定改變派遣計劃，具體規則為：把原計劃擬派遣的各批人數依次構成的數列記為{a_n}，在數列{a_n}的任意相鄰兩項a_k與a_k+1（k=1，2，?）之間插入3^k個2，使它們和原數列的項構成一個新的數列{b_n}．按新數列{b_n}的各項依次派遣支教學生．記S₅₀為派遣了50批學生后參加公益活動學生的總數，則S₅₀的值為（　　）

  A．198

  B．200

  C．240

  D．242
  組卷：55引用：1難度：0.6

  解析

• 7．已知圓C：x²+y²=1，橢圓Γ：

  x

  2

  4

  +

  y

  2

  3

  =1，過C上任意一點P作圓C的切線l,交Γ于A，B兩點，過A，B分別作橢圓Γ的切線，兩切線交于點Q，則|OQ|（O為坐標原點）的最大值為（　　）

  A．16

  B．8

  C．4

  D．2
  組卷：115引用：4難度：0.5

  解析

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

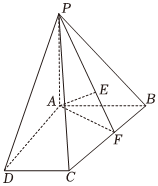• 21．如圖，在四棱錐P-ABCD中，PA⊥底面ABCD，AD⊥AB，AB∥DC，∠ABC=

  π

  3

  ，AB=BC，PA=2．點A在平面PBC內的投影恰好為△PBC的重心E，連接PE并延長交BC于F．
  （Ⅰ）求證：AF⊥BC；
  （Ⅱ）求平面ACE與平面ABCD所成夾角的余弦值．
  組卷：73引用：3難度：0.4

  解析

• 22．已知雙曲線C：x²-y²=λ（λ＞0），焦點F到其中一條漸近線的距離為

  3

  ．
  （Ⅰ）求：λ；
  （Ⅱ）動點M，N在曲線C上，已知點A（2，-1），直線AM，AN分別與y軸相交的兩點關于原點對稱，點Q在直線MN上，AQ⊥MN，證明：存在定點T，使得|QT|為定值．
  組卷：61引用：1難度：0.4

  解析