2022-2023學年云南省大理州大理市下關一中教育集團高二（上）段考數學試卷（二）（A卷）

一、單項選擇題（本大題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．若i（1-z）=1，則z+

  z

  =（　　）

  A．-2

  B．-1

  C．1

  D．2
  組卷：5792引用：18難度：0.9

  解析

• 2．直線

  3

  x+y+2=0的傾斜角為（　　）

  A． π 6

  B． π 3

  C． 2 π 3

  D． 5 π 6
  組卷：13引用：1難度：0.9

  解析

• 3．在等差數列{a_n}中，已知a₁=2，a₃=8，則a₄+a₅+a₆等于（　　）

  A．40

  B．42

  C．43

  D．45
  組卷：30引用：5難度：0.8

  解析

• 4．在等比數列{a_n}中，a₃，a₁₅是方程x²+6x+2=0的根，則

  a

  2

  a

  16

  a

  9

  的值為（　　）

  A．- 2 + 2 2

  B． - 2

  C． 2

  D． - 2 或 2
  組卷：304引用：14難度：0.7

  解析

• 5．數學家蒙日發現：橢圓上兩條互相垂直的切線的交點必在一個與橢圓同心的圓上，且圓半徑的平方等于長半軸、短半軸的平方和，此圓被命名為該橢圓的蒙日圓．若圓

  x

  2

  12

  +

  y

  2

  b

  2

  =

  1

  的蒙日圓為x²+y²=20，則該橢圓的離心率為（　　）

  A． 3 3

  B． 1 3

  C． 2 3

  D． 6 3
  組卷：53引用：4難度：0.7

  解析

• 6．已知拋物線型拱橋的頂點距水面2米時，測量得水面寬8米．當水面升高0.5米后，水面寬度是（　　）米

  A．3

  B．4

  C． 3 3

  D． 4 3
  組卷：54引用：4難度：0.7

  解析

• 7．已知雙曲線

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的右焦點為

  F

  （

  4

  3

  ，

  0

  ）

  ，過F和P（0，2b）兩點的直線與雙曲線的一條漸近線平行，則該雙曲線的方程為（　　）

  A． x 2 36 - y 2 12 = 1	B． x 2 12 - y 2 36 = 1
  C． x 2 16 - y 2 32 = 1	D． x 2 32 - y 2 16 = 1
  組卷：1引用：3難度：0.5

  解析

四、解答題（共70分.解答應寫出文字說明，證明過程或演算步驟）

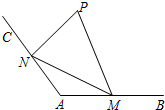• 21．如圖，為方便市民游覽市民中心附近的“網紅橋”，現準備在河岸一側建造一個觀景臺P，已知射線AB，AC為兩邊夾角為120°的公路（長度均超過3千米），在兩條公路AB，AC上分別設立游客上下點M，N，從觀景臺P到M，N建造兩條觀光線路PM，PN，測得AM=

  3

  千米，AN=

  3

  千米．
  （1）求線段MN的長度；
  （2）若∠MPN=60°，求兩條觀光線路PM與PN所圍成△PMN的面積的最大值．
  組卷：63引用：3難度：0.7

  解析

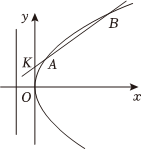• 22．設拋物線y²=2px（p＞0）的準線為l,A、B為拋物線上兩動點，AA'⊥l于A'，定點K（0，1）使|KA|+|AA'|有最小值

  2

  ．
  （1）求拋物線的方程；
  （2）當

  KA

  =

  λ

  KB

  （λ∈R且λ≠1）時，是否存在一定點T滿足

  TA

  ?

  TB

  為定值？若存在，求出T的坐標和該定值；若不存在，請說明理由．
  組卷：97引用：4難度：0.5

  解析