2022-2023學年浙江省寧波市南三縣八年級(上)期末數學試卷
發布:2024/12/27 16:30:3
一、選擇題(共10小題,每小題3分,滿分30分)
-
1.若三角形兩邊長分別為2,6,則該三角形第三邊長可能是( )
A.3 B.4 C.5 D.9 組卷:446引用:9難度:0.6 -
2.用數學的眼光觀察下面的網絡圖標,其中可以抽象成軸對稱圖形的是( )
A. 
B. 
C. 
D.  組卷:53引用:1難度:0.9
組卷:53引用:1難度:0.9 -
3.點A(-2,y1),B(3,y2)在一次函數y=x+b的圖象上,y1與y2的大小關系是( )
A.y1>y2 B.y1=y2 C.y1<y2 D.y1≥y2 組卷:953引用:6難度:0.8 -
4.若點A(-a,b)在第一象限,則點B(a,b)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限 組卷:1873引用:9難度:0.7 -
5.當b>0時,一次函數y=x+b的大致圖象是( )
A. 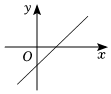
B. 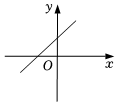
C. 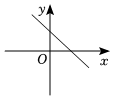
D. 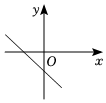 組卷:874引用:5難度:0.6
組卷:874引用:5難度:0.6 -
6.下列命題的逆命題是假命題的是( )
A.直角三角形的兩個銳角互余 B.兩直線平行,內錯角相等 C.三條邊對應相等的兩個三角形是全等三角形 D.若x=y,則x2=y2 組卷:433引用:4難度:0.6 -
7.如圖,在△ABC中,∠ACB=2∠B,下列尺規作圖,不能得到∠ADC=2∠B的是( )
A. 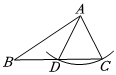
B. 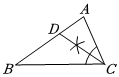
C. 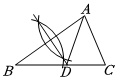
D. 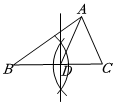 組卷:913引用:17難度:0.5
組卷:913引用:17難度:0.5 -
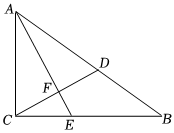 8.如圖,在△ABC中,∠ACB=90°,AC=6,BC=8,點D在邊AB上,AD=AC,AE⊥CD,垂足為F,與BC交于點E,則BE的長是( )
8.如圖,在△ABC中,∠ACB=90°,AC=6,BC=8,點D在邊AB上,AD=AC,AE⊥CD,垂足為F,與BC交于點E,則BE的長是( )A.3 B.5 C. 163D.6 組卷:2949引用:5難度:0.4
三、解答題(8小題,共66分)
-
23.定義:在任意△ABC中,如果一個內角度數的2倍與另一個內角度數的和為90°,那么稱此三角形為“倍角互余三角形.
【基礎鞏固】(1)若△ABC是“倍角互余三角形”,∠C>90°,∠A=60°,則∠B=°;
【嘗試應用】(2)如圖1,在Rt△ABC中,∠ACB=90°,點D為線段BC上一點,若∠CAD與∠CAB互余.求證:△ABD是“倍角互余三角形”;
【拓展提高】(3)如圖2,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,試問在邊BC上是否存在點E,使得△ABE是“倍角互余三角形”?若存在,請求出BE的長;若不存在,請說明理由.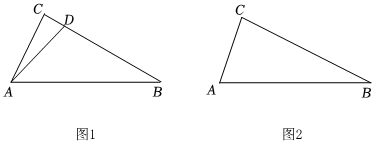 組卷:336引用:1難度:0.1
組卷:336引用:1難度:0.1 -
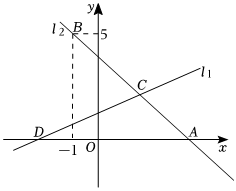 24.如圖,直線l1:y=kx+1與x軸交于點D,直線l2:y=-x+b與x軸交于點A,且經過定點B(-1,5),直線l1與l2交于點C(2,m).
24.如圖,直線l1:y=kx+1與x軸交于點D,直線l2:y=-x+b與x軸交于點A,且經過定點B(-1,5),直線l1與l2交于點C(2,m).
(1)填空:k=;b=;m=;
(2)在x軸上是否存在一點E,使△BCE的周長最短?若存在,請求出點E的坐標;若不存在,請說明理由.
(3)若動點P在射線DC上從點D開始以每秒1個單位的速度運動,連接AP,設點P的運動時間為t秒,是否存在t的值,使△ACP和△ADP的面積比為1:2?若存在,直接寫出t的值;若不存在,請說明理由.組卷:748引用:1難度:0.3


