2023-2024學年新疆昌吉州昌吉一中高二（上）期中數學試卷

一、單項選擇題（本大題共8小題，每題5分，共40分，在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．經過

  A

  （

  0

  ，

  3

  ）

  ，B（3，0）兩點的直線的傾斜角為（　　）

  A． 5 π 6

  B． π 6

  C． 2 π 3

  D． π 3
  組卷：187引用：15難度：0.9

  解析

• 2．已知直線x-y+2=0與圓（x-1）²+（y-2）²=4交于A，B兩點，則|AB|=（　　）

  A． 14

  B． 15

  C． 2 3

  D．4
  組卷：16引用：3難度：0.6

  解析

• 3．已知直線l₁：ax+（a+2）y+1=0，l₂：x+ay+2=0，其中a∈R，則“a=-3”是“l₁⊥l₂”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：74引用：7難度：0.9

  解析

• 4．在長方體ABCD-A₁B₁C₁D₁中，AB=1，AD=2，AA₁=3，則

  BD

  ?

  A

  C

  1

  =（　　）

  A．1

  B．0

  C．3

  D．-3
  組卷：21引用：5難度：0.9

  解析

• 5．已知向量

  a

  +

  b

  =

  （

  0

  ，

  2

  ，

  0

  ）

  ，

  a

  -

  b

  =

  （

  2

  ，

  2

  ，-

  2

  3

  ）

  ，則

  cos

  ?

  a

  ，

  b

  ?

  =（　　）

  A． - 6 3

  B． 6 3

  C． - 6 6

  D． 6 6
  組卷：135引用：5難度：0.7

  解析

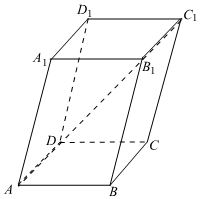• 6．如圖，在平行六面體ABCD-A₁B₁C₁D₁中，底面ABCD是邊長為1的正方形，側棱AA₁=2且∠A₁AD=∠A₁AB=60°，則AC₁=（　　）

  A． 2 2

  B． 10

  C． 2 3

  D． 14
  組卷：241引用：18難度：0.7

  解析

• 7．若雙曲線

  y

  2

  2

  -

  x

  2

  m

  =

  1

  的焦點與橢圓

  x

  2

  3

  +

  y

  2

  4

  =

  1

  的長軸端點重合，則m的值為（　　）

  A．2

  B．4

  C．-2

  D．-4
  組卷：157引用：5難度：0.8

  解析

四、解答題（本大題共6小題，第17題10分，第18-22題每小題10分，共70分，解答應寫出文字說明、證明過程或演算步驟）

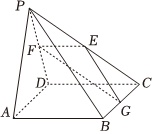• 21．如圖，在四棱錐P-ABCD中，底面ABCD是邊長為4的正方形，△PAD是正三角形，CD⊥平面PAD，E，F，G分別是PC，PD，BC的中點．
  （1）求證：平面PAD⊥平面ABCD．
  （2）線段PA上是否存在點M，使得直線GM與平面EFG所成角為

  π

  6

  ？若存在，求線段PM的長度；若不存在，請說明理由．
  組卷：225引用：13難度：0.4

  解析

• 22．已知圓

  C

  1

  ：

  （

  x

  +

  3

  ）

  2

  +

  y

  2

  =

  9

  ，

  C

  2

  ：

  （

  x

  -

  3

  ）

  2

  +

  y

  2

  =

  1

  ，動圓M與圓C₁，C₂均外切，記圓心M的軌跡為曲線C．
  （1）求曲線C的方程；
  （2）直線l過點C₂，且與曲線C交于A，B兩點，滿足

  A

  C

  2

  =

  3

  C

  2

  B

  ，求直線l的方程．
  組卷：143引用：8難度：0.4

  解析