2022年山西省呂梁市高考數學二模試卷（理科）

一、選擇題：本題共12小題，每小題5分，共60分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．設全集U=R，集合A={x|1≤x≤3}，B={0，1，2，3，4，5}，則（?_UA）∩B=（　　）

  A．{0，4，5}

  B．{0，1，3，4，5}

  C．{4，5}

  D．{0}
  組卷：153引用：5難度：0.8

  解析

• 2．已知復數

  z

  =

  4

  i

  3

  +

  i

  ，則

  z

  =（　　）

  A． 3 - i

  B． 1 + 3 i

  C． 1 - 3 i

  D． 3 + i
  組卷：57引用：2難度：0.8

  解析

• 3．如圖是某地區2001年至2021年環境保護建設投資額（單位：萬元）的折線圖．
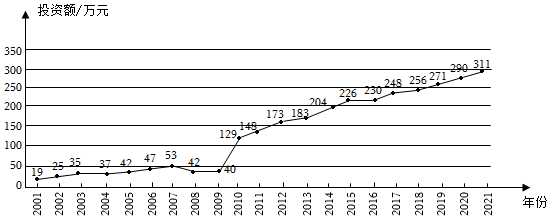
  根據該折線圖判斷，下列結論正確的是（　　）

  A．為預測該地2022年的環境保護建設投資額，應用2001年至2021年的數據建立回歸模型更可靠

  B．為預測該地2022年的環境保護建設投資額，應用2010年至2021年的數據建立回歸模型更可靠

  C．投資額與年份負相關

  D．投資額與年份的相關系數r＜0
  組卷：127引用：3難度：0.8

  解析

• 4．為得到函數y=cos2x的圖象，只需將函數

  y

  =

  cos

  （

  2

  x

  +

  π

  5

  ）

  的圖象（　　）

  A．向右平移 π 5 個單位長度

  B．向左平移 π 5 個單位長度

  C．向右平移 π 10 個單位長度

  D．向左平移 π 10 個單位長度
  組卷：135引用：1難度：0.8

  解析

• 5．如圖是我國古代量糧食的器具“升”，其形狀是正四棱臺，上、下底面邊長分別為15cm和10cm,高為15cm.“升”裝滿后用手指或筷子沿升口刮平，這叫“平升”．則該“升”的“平升”約可裝（1000cm³=1L）（　　）

  A．1.9L

  B．2.2L

  C．2.4L

  D．4.6L
  組卷：215引用：6難度：0.8

  解析

• 6．函數

  f

  （

  x

  ）

  =

  3

  sin

  3

  x

  3

  x

  +

  3

  -

  x

  的部分圖象大致為（　　）

  A．	B．
  C．	D．
  組卷：414引用：5難度：0.8

  解析

• 7．已知點F為拋物線C：y²=8x的焦點，過F的直線l與C交于A，B兩點．若AB中點的縱坐標為2，則|AB|=（　　）

  A．6

  B．7

  C．9

  D．10
  組卷：97引用：2難度：0.6

  解析

（二）選考題：共10分．請考生在第22、23題中任選一題作答，如果多做，則按所做的第一題計分．[選修4-4：坐標系與參數方程]

• 22．在平面直角坐標系xOy中，以坐標原點O為極點、x軸的正半軸為極軸建立極坐標系，曲線C的極坐標方程為ρ²（1+3sin²θ）=16，曲線C₁的極坐標方程為2ρcosθ+3ρsinθ=20．
  （1）求曲線C和C₁的直角坐標方程，并分別說明表示什么曲線；
  （2）若點A為曲線C上的動點，點B為曲線C₁上的動點，點M為P（-4，4）和A的中點，求|MB|的最小值．
  組卷：111引用：1難度：0.5

  解析

[選修4-5：不等式選講]

• 23．已知函數

  f

  （

  x

  ）

  =

  |

  x

  +

  2

  a

  |

  +

  |

  x

  -

  2

  a

  |

  （

  a

  ＞

  0

  ）

  ．
  （1）當a=1時，解不等式f（x）≤6；
  （2）若f（x）≥5恒成立，求實數a的取值范圍．
  組卷：95引用：6難度：0.6

  解析