2022-2023學(xué)年河北省保定市高碑店市崇德實(shí)驗(yàn)中學(xué)高二（下）期中數(shù)學(xué)試卷

一、單選題（本大題共8小題，每小題5分，共40分.在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的）.

• 1．已知集合A={x|-1＜x＜2}，B={x|0＜x＜3}，則A∪B=（　　）

  A．（-1，3）

  B．（-1，0）

  C．（0，2）

  D．（2，3）
  組卷：4707引用：83難度：0.9

  解析

• 2．在下列各圖中的兩個(gè)變量具有線性相關(guān)關(guān)系的圖是（　　）
  

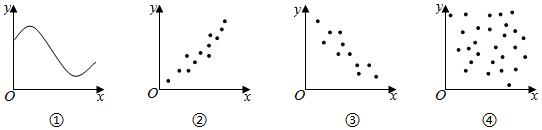
  A．①②

  B．①③

  C．②③

  D．②④
  組卷：410引用：3難度：0.9

  解析

• 3．設(shè)隨機(jī)變量X～B（5，

  1

  3

  ），則D（3X）=（　　）

  A．10

  B．30

  C．15

  D．5
  組卷：290引用：3難度：0.6

  解析

• 4．求（x²+2）（

  1

  x

  -

  1

  ）⁶的展開(kāi)式的常數(shù)項(xiàng)是（　　）

  A．15

  B．-15

  C．17

  D．-17
  組卷：122引用：5難度：0.9

  解析

• 5．某班聯(lián)歡會(huì)原定3個(gè)節(jié)目已排成節(jié)目單，開(kāi)演前又增加了2個(gè)節(jié)目，如果將這2個(gè)新節(jié)目插入節(jié)目單中，那么不同的插法種數(shù)為（　　）

  A．12

  B．20

  C．24

  D．30
  組卷：201引用：2難度：0.7

  解析

• 6．下列說(shuō)法中，正確的命題的是（　　）

  A．一臺(tái)晚會(huì)有6個(gè)節(jié)目，其中有2個(gè)小品，如果2個(gè)小品不連續(xù)演出，共有不同的演出順序240種．

  B．以模型y=cekx去擬合一組數(shù)據(jù)時(shí)，為了求出回歸方程，設(shè)z=lny,求得線性回歸方程為 ? z = 0 . 3 x + 4 ，則c,k的值分別是e4和0.3

  C．若事件A與事件B互斥，則事件A與事件B獨(dú)立

  D．若樣本數(shù)據(jù)x1，x2，…，x10的方差為2，則數(shù)據(jù)2x1-1，2x2-1，…，2x10-1的方差為1
  組卷：78引用：1難度：0.5

  解析

• 7．已知曲線y=xlnx+ae^-x在點(diǎn)x=1處的切線方程為2x-y+b=0，則b=（　　）

  A．-1

  B．-2

  C．-3

  D．0
  組卷：386引用：4難度：0.7

  解析

四、解答題：（本題共有六道小題，共70分.解答應(yīng)寫(xiě)出文字說(shuō)明，證明過(guò)程或演算步驟.

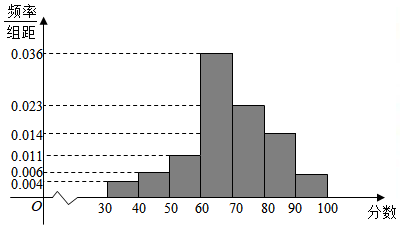• 21．2021年是中國(guó)共產(chǎn)黨百年華誕．中國(guó)站在“兩個(gè)一百年”的歷史交匯點(diǎn)，全面建設(shè)社會(huì)主義現(xiàn)代化國(guó)家新征程即將開(kāi)啟.2021年3月23日，中宣部介紹中國(guó)共產(chǎn)黨成立100周年慶祝活動(dòng)八項(xiàng)主要內(nèi)容，其中第一項(xiàng)是結(jié)合鞏固深化“不忘初心，牢記使命”主題教育成果，在全體黨員中開(kāi)展黨史學(xué)習(xí)教育．這次學(xué)習(xí)教育貫穿2021年全年，總的要求是學(xué)史明理，學(xué)史增信、學(xué)史崇德，學(xué)史力行，教育引導(dǎo)黨員干部學(xué)黨史、悟思想、辦實(shí)事，開(kāi)新局．為了配合這次學(xué)黨史活動(dòng)，某地組織全體黨員干部參加黨史知識(shí)競(jìng)賽，現(xiàn)從參加人員中隨機(jī)抽取100人，并對(duì)他們的分?jǐn)?shù)進(jìn)行統(tǒng)計(jì)，得到如圖所示的頻率分布直方圖．
  （1）現(xiàn)從這100人中隨機(jī)抽取2人，記其中得分不低于80分的人數(shù)為ξ，試求隨機(jī)變量ξ的分布列及期望；
  （2）由頻率分布直方圖，可以認(rèn)為該地參加黨史知識(shí)競(jìng)賽人員的分?jǐn)?shù)X服從正態(tài)分布N（μ，σ²），其中μ近似為樣本平均數(shù)，σ²近似為樣本方差s²，經(jīng)計(jì)算s²=192.44．現(xiàn)從所有參加黨史知識(shí)競(jìng)賽的人員中隨機(jī)抽取500人，且參加黨史知識(shí)競(jìng)賽的人員的分?jǐn)?shù)相互獨(dú)立，試問(wèn)這500名參賽者的分?jǐn)?shù)高于82.3的人數(shù)最有可能是多少？
  （參考數(shù)據(jù)：

  192

  .

  44

  ≈

  13

  .

  9

  ，P（μ-σ≤X≤μ+σ）=0.6827，P（μ-2σ≤X≤μ+2σ）=0.9545，P（μ-3σ≤X≤μ+3σ）=0.9973）
  組卷：27引用：1難度：0.5

  解析

• 22．函數(shù)f（x）=lnx,g（x）=x²-x-m+2．
  （Ⅰ）若m=e,求函數(shù)F（x）=f（x）-g（x）的最大值；
  （Ⅱ）若f（x）+g（x）≤x²-（x-2）e^x在x∈[0，2）恒成立，求實(shí)數(shù)m的取值范圍．
  組卷：37引用：4難度：0.5

  解析