當前位置：試卷中心 > 試卷詳情

1991年第2屆“希望杯”全國數學邀請賽試卷（初二第2試）

發布：2024/4/20 14:35:0

1．如圖，已知B是線段AC上的一點，M是線段AB的中點，N是線段AC的中點，P為NA的中點，Q是AM的中點，則MN：PQ等于（　　）
A．1 B．2 C．3 D．4
組卷：1939引用：19難度：0.7
解析
2．兩個正數m,n的比是t（t＞1）．若m+n=s,則m,n中較小的數可以表示為（　　）
A．ts B．s-ts C．
ts
1
+
s
D．
s
1
+
t
組卷：76引用：1難度：0.7
解析
3．y＞0時，
-
x
3
y
等于（　　）
A．-x
xy
B．x
xy
C．-x
-
xy
D．x
-
xy
組卷：60引用：1難度：0.9
解析
4．（x+a）（x+b）+（x+b）（x+c）+（x+c）（x+a）是完全平方式，則a,b,c的關系可以寫成（　　）
A．a＜b＜c B．（a-b）²+（b-c）²=0
C．c＜a＜b D．a=b≠c
組卷：899引用：2難度：0.5
解析
5．如圖，AC=CD=DA=BC=DE．則∠BAE是∠BAC的（　　）
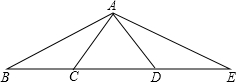
A．4倍 B．3倍 C．2倍 D．1倍
組卷：425引用：4難度：0.9
解析
6．D是等腰銳角三角形ABC的底邊BC上一點，則AD，BD，CD滿足關系式（　　）
A．AD²=BD²+CD² B．AD²＞BD²+CD²
C．2AD²=BD²+CD² D．2AD²＞BD²+CD²
組卷：698引用：1難度：0.5
解析
7．方程
|
x
2
-
1
|
=
1
10
（
x
+
9
10
）
的實根個數為（　　）
A．4 B．3 C．2 D．1
組卷：48引用：1難度：0.9
解析

21．已知兩個正數的立方和是最小的質數．求證：這兩個數之和不大于2．
組卷：49引用：1難度：0.1
解析
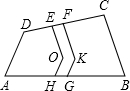22．一塊四邊形的地（如圖）（EO∥FK，OH∥KG）內有一段曲折的水渠，現在要把這段水渠EOHGKF改成直的．（即兩邊都是直線）但進水口EF的寬度不能改變，新渠占地面積與原水渠面積相等，且要盡可能利用原水渠，以節省工時．那么新渠的兩條邊應當怎么作？寫出作法，并加以證明．
組卷：118引用：1難度：0.1
解析