2023年江西省鷹潭市高考數學二模試卷（理科）

一、選擇題：本大題共12小題，每小題5分，共60分.在每小題給出的四個選項中，只有一項是符

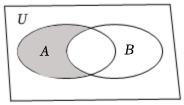• 1．如圖，兩個區域分別對應集合A，B，其中A={-2，-1，0，1，2}，B={x∈N|x＜4}．則陰影部分表示的集合為（　　）

  A．{0，1，2}

  B．{0，1}

  C．{-2，-1，2}

  D．{-2，-1}
  組卷：68引用：3難度：0.7

  解析

• 2．若復數z滿足

  i

  ?

  z

  =

  2022

  +

  i

  2023

  （i是虛數單位），z的共軛復數是

  z

  ，則

  z

  -

  z

  的模是（　　）

  A． 4044 2 + 4

  B．4044

  C．2

  D．0
  組卷：83引用：3難度：0.9

  解析

• 3．下列命題中錯誤的是（　　）

  A．命題“ ? x 0 ∈ R ， x 2 0 + 1 ＜ 1 ”的否定是“?x∈R，x2+1≥1”

  B．命題“若a＞b,則2a＞2b-1”的否命題為“若a≤b,則2a≤2b-1”

  C．“兩直線斜率相等”是“兩直線平行”的充要條件

  D．若“p或q”為假命題，則p,q均為假命題
  組卷：68引用：2難度：0.7

  解析

• 4．已知a=log₃9，

  b

  =

  e

  ln

  1

  2

  ，

  c

  =

  3

  2

  執行如圖所示的程序框圖，輸出的值為（　　）
  

  A．2

  B． 1 2

  C． 3 2

  D．1
  組卷：1引用：2難度：0.9

  解析

• 5．若sin（α+β）+cos（α+β）=2

  2

  cos（α+

  π

  4

  ）sinβ，則（　　）

  A．tan（α-β）=1	B．tan（α+β）=1
  C．tan（α-β）=-1	D．tan（α+β）=-1
  組卷：6967引用：18難度：0.6

  解析

• 6．已知等差數列{a_n}滿足

  a

  2

  1

  +

  a

  2

  4

  =

  4

  ，則a₂+a₃可能取的值是（　　）

  A．-2

  B．-3

  C．4

  D．6
  組卷：115引用：3難度：0.7

  解析

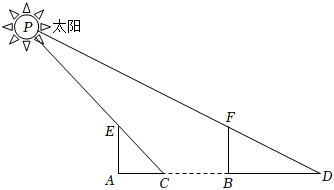• 7．“寸影千里”法是《周髀算經》中記載的一種遠距離測量的估算方法，其具體方法是在同一天（如夏至）的正午，于兩地分別豎起同高的標桿，然后測量標桿的影長，并根據“日影差一寸，實地相距千里”的原則推算兩地距離．如圖，某人在夏至的正午分別在同一水平面上的A，B兩地豎起高度均為a寸的標桿AE與BF，AC與BD的差結合“寸影千里”來推算A，B兩地的距離．記

  ∠

  CEA

  =

  α

  ，

  ∠

  BDF

  =

  β

  （

  β

  ＜

  π

  2

  -

  α

  ）

  ，則按照“寸影千里”的原則，A，B兩地的距離大約為（　　）

  A． 1000 asin （ α + β ） sinαsinβ 里

  B． 1000 asin （ α + β ） sinαcosβ 里

  C． 1000 acos （ α + β ） sinβcosα 里

  D． 1000 acos （ α + β ） cosαcosβ 里
  組卷：209引用：8難度：0.5

  解析

選考題：共10分．請考生在第22、23題中任選一題作答．如果多做，則按所做的第一題計分．[選修4-4：坐標系與參數方程]

• 22．在平面直角坐標系xOy中，以原點O為極點，x軸的正半軸為極軸建立極坐標系，曲線C₁的極坐標方程為ρ=2cosθ，曲線C₂的極坐標方程為

  ρ

  =

  2

  2

  5

  +

  3

  cos

  2

  θ

  ．
  （1）寫出曲線C₂的參數方程；
  （2）設A是曲線C₁上的動點，B是曲線C₂上的動點，求A，B之間距離的最大值．
  組卷：133引用：5難度：0.6

  解析

[選修4-5：不等式選講]

• 23．已知m＞0，n＞0，m²+n²=4m²n²．
  （1）證明：

  （

  m

  1

  2

  +

  n

  1

  2

  ）

  （

  m

  3

  2

  +

  n

  3

  2

  ）

  ≥

  2

  ；
  （2）證明：

  1

  m

  4

  +

  1

  n

  4

  ≥

  8

  ．
  組卷：19引用：3難度：0.6

  解析