2022-2023學(xué)年湖南省邵陽(yáng)市邵東一中高三（上）第二次月考數(shù)學(xué)試卷

一、單項(xiàng)選擇題（本題共8小題，每小題5分，共40分）

• 1．設(shè)A={x∈Z|x≤5}，B={x∈Z|x＞1}，那么A∩B等于（　　）

  A．{1，2，3，4，5}

  B．{2，3，4，5}

  C．{2，3，4}

  D．{x|1＜x≤5}
  組卷：85引用：12難度：0.9

  解析

• 2．已知

  a

  =

  lo

  g

  3

  2

  ，

  b

  =

  6

  0

  .

  03

  ，

  c

  =

  lo

  g

  4

  5

  ×

  lo

  g

  5

  2

  ，則（　　）

  A．c＜b＜a

  B．b＜c＜a

  C．c＜a＜b

  D．a(chǎn)＜c＜b
  組卷：306引用：5難度：0.7

  解析

• 3．“cosα=

  3

  5

  ”是“sin（2α+

  π

  2

  ）=-

  7

  25

  ”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：129引用：8難度：0.8

  解析

• 4．函數(shù)y=ln（e^x+e^-x）的圖像大致是（　　）

  A．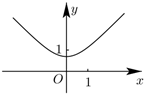

  B．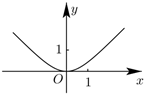

  C．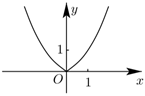

  D．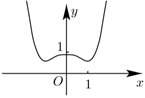
  組卷：100引用：6難度：0.7

  解析

• 5．已知

  sin

  （

  π

  3

  -

  α

  2

  ）

  =

  -

  3

  2

  ，則

  cos

  （

  π

  3

  +

  α

  ）

  =（　　）

  A． 3 2

  B． - 3 2

  C． 1 2

  D．- 1 2
  組卷：47引用：4難度：0.9

  解析

• 6．已知等差數(shù)列{a_n}的前n項(xiàng)和為S_n，若a₁=-2022，且

  S

  2023

  2023

  -

  S

  2022

  2022

  =

  1

  ，則S₂₀₂₃=（　　）

  A．0

  B．1

  C．2022

  D．2023
  組卷：346引用：3難度：0.7

  解析

• 7．設(shè)函數(shù)f（x）=sin（ωx+

  π

  3

  ）在區(qū)間（0，π）恰有三個(gè)極值點(diǎn)、兩個(gè)零點(diǎn)，則ω的取值范圍是（　　）

  A．[ 5 3 ， 13 6 ）

  B．[ 5 3 ， 19 6 ）

  C．（ 13 6 ， 8 3 ]

  D．（ 13 6 ， 19 6 ]
  組卷：6765引用：17難度：0.6

  解析

四、解答題（本題共6題，共10+12+12+12+12+12=70分）

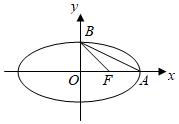• 21．如圖，已知橢圓C的離心率為

  3

  2

  ，點(diǎn)A，B，F(xiàn)分別為橢圓的右頂點(diǎn)、上頂點(diǎn)和右焦點(diǎn)，且S_△ABF=1-

  3

  2

  ．
  （1）求橢圓C的方程；
  （2）已知直線l：y=kx+m與圓O：x²+y²=1相切，若直線l與橢圓C交于M，N兩點(diǎn)，求△OMN面積的最大值．
  組卷：127引用：3難度：0.6

  解析

• 22．設(shè)f（x）=e^xsinx.
  （1）求f（x）在[-π，π]上的極值；
  （2）若對(duì)?x₁，x₂∈[0，π]，x₁≠x₂，都有

  f

  （

  x

  1

  ）

  -

  f

  （

  x

  2

  ）

  x

  2

  1

  -

  x

  2

  2

  +

  a

  ＞

  0

  成立，求實(shí)數(shù)a的取值范圍．
  組卷：213引用：9難度：0.4

  解析