當前位置：試卷中心 > 試卷詳情

2022-2023學年江西省贛州市全南中學高一（下）期中數學試卷

發布：2024/4/28 8:51:19

一、單選題（每題5分，共40分）

1．“?x∈R，x²+ax+1≥0成立”是“|a|≤2”的（　　）
A．充分必要條件 B．必要而不充分條件
C．充分而不必要條件 D．既不充分也不必要條件
組卷：53引用：2難度：0.9
解析
2．設
a
0
，
b
0
分別是
a
，
b
的單位向量，則下列結論中正確的是（　　）
A．
a
0
=
b
0
B．
a
0
?
b
0
=1 C．
|
a
0
|
+
|
b
0
|
=2 D．|
a
0
+
b
0
|=2
組卷：155引用：11難度：0.9
解析
3．函數y=3sinx+5（-
π
2
≤x≤0）最大值為（　　）
A．2 B．5 C．8 D．7
組卷：386引用：2難度：0.7
解析
4．已知O是四邊形ABCD所在平面內的一點，且
OA
，
OB
，
OC
，
OC
滿足等式
OA
+
OC
=
OB
+
OD
，則四邊形ABCD是（　　）
A．平行四邊形 B．菱形 C．梯形 D．等腰梯形
組卷：32引用：1難度：0.8
解析
5．已知α，β均為銳角，且
cos
（
α
+
β
）
=
sinα
sinβ
，則tanα的最大值是（　　）
A．4 B．2 C．
2
4
D．
2
5
組卷：356引用：5難度：0.7
解析
6．已知
tan
（
θ
+
π
4
）
=
3
，則cos2θ=（　　）
A．
-
4
5
B．0 C．
4
5
D．
3
5
組卷：37引用：1難度：0.7
解析
7．已知函數
f
（
x
）
=
sin
（
ωx
+
φ
）
（
ω
＞
0
，
|
φ
|
＜
π
2
）
，其圖象相鄰兩條對稱軸之間的距離為
π
2
，將函數y=f（x）的圖象向左平移
π
8
個單位后，得到的圖象關于原點對稱，那么函數y=f（x）在
[
0
，
π
2
]
上的值域是（　　）
A．
[
-
2
2
，
2
2
]
B．
[
-
2
2
，
1
]
C．
[
0
，
2
2
]
D．[0，1]
組卷：31引用：2難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題（共70分）

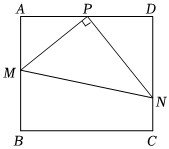21．某公園有一塊矩形空地ABCD，其中AB⊥BC，
AB
=
3
百米，BC=2百米．為迎接“五一”觀光游，欲從邊界AD上的中點P處開始修建觀賞小徑PM，PN，MN，其中M，N分別在邊界AB，CD上，小徑PM與PN相互垂直，區域PMA和區域PND內種植繡球花，區域PMN內種植玫瑰花，區域BMNC內種植杜鵑花．設∠APM=α．
（1）設種植繡球花的區域的面積為S，試將S表示為關于α的函數，并求其取值范圍；
（2）為了節省建造成本，公園負責人要求觀賞小徑的長度之和（即△PMN的周長l）最小．試分析當α為何值時，△PMN的周長l最小，并求出其最小值．
組卷：69引用：4難度：0.6
解析
22．若函數f（x）滿足
f
（
x
-
π
2
）
=
f
（
x
+
π
2
）
，且f（a-x）=f（x+a），a∈R，則稱f（x）為“M型a函數”．
（1）判斷函數
y
=
sin
（
2
x
-
π
4
）
是否為“M型
3
π
8
函數”，并說明理由；
（2）已知g（x）為定義域為R的奇函數，當x＞0時，g（x）=lnx,函數h（x）為“M型
π
6
函數”，當
x
∈
[
-
π
3
，
π
6
]
時，h（x）=2cos2x,若函數F（x）=g（h（x）-m）（m∈R）在
[
-
5
π
6
，
2
π
3
]
上的零點個數為9，求m的取值范圍．
組卷：79引用：6難度：0.6
解析