2022年山西省長治市名校高考數學模擬試卷（理科）

一、選擇題：本題共12小題，每小題5分，共60分。在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．已知集合P={s|s=2k+1，k∈Z}，Q={s|s=4k+1，k∈Z}，則P∩Q=（　　）

  A．P

  B．Q

  C．Z

  D．?
  組卷：20引用：2難度：0.7

  解析

• 2．若

  z

  =

  i

  3

  i

  +

  1

  ，則|z|=（　　）

  A． 1 10

  B．10

  C． 10 10

  D． 10
  組卷：113引用：3難度：0.9

  解析

• 3．命題P：?x≤0，x²-2x+e＞1，則￢P為（　　）

  A．?x＞0，x2-2x+e≤1	B．?x≤0，x2-2x+e≤1
  C．?x＞0，x2-2x+e≤1	D．?x≤0，x2-2x+e≤1
  組卷：122引用：5難度：0.9

  解析

• 4．若函數f（x）滿足f（x+2）=f（x），則f（x）可以是（　　）

  A．f（x）=（x-1）2	B．f（x）=|x-2|
  C．f（x）=sin（ π 2 x ）	D．f（x）=tan（ π 2 x ）
  組卷：51引用：4難度：0.8

  解析

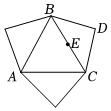• 5．如圖，某幾何體平面展開圖由一個等邊三角形和三個等腰直角三角形組合而成，E為BC的中點，則在原幾何體中，異面直線AE與CD所成角的余弦值為（　　）

  A． 6 3

  B． 6 6

  C． 3 3

  D． 6 12
  組卷：219引用：12難度：0.5

  解析

• 6．

  （

  x

  2

  -

  2

  x

  +

  1

  x

  ）

  （

  1

  -

  2

  x

  ）

  5

  展開式中常數項為（　　）

  A．-15

  B．0

  C．15

  D．80
  組卷：236引用：3難度：0.7

  解析

• 7．已知α∈（-π，0），且3cos2α-2sinαcosα-3=0，則sinα=（　　）

  A． 3 10 10

  B． 10 10

  C． - 3 10 10

  D． - 10 10
  組卷：155引用：2難度：0.7

  解析

（二）選考題：共10分。請考生在第22、23題中任選一題作答。如果多做，則按所做的第一題計分。[選修4-4：坐標系與參數方程]

• 22．在直角坐標系xOy中，以坐標原點為極點，以x軸正半軸為極軸，建立極坐標系，直線l的極坐標方程為

  ρcos

  （

  θ

  -

  π

  3

  ）

  =

  3

  2

  ，曲線C的極坐標方程為ρ²（3-cos2θ）=8．
  （1）寫出直線l和曲線C的直角坐標方程；
  （2）已知點

  P

  （

  3

  ，

  0

  ）

  ，若直線l與畫線C交于A，B兩點，求

  1

  |

  PA

  |

  +

  1

  |

  PB

  |

  的值．
  組卷：80引用：6難度：0.7

  解析

[選修4-5：不等式選講]（10分）

• 23．已知f（x）=|2x-a²|．
  （1）當a=1時，求不等式f（x）+|x+1|≥3的解集；
  （2）若對于任意實數x,不等式|2x-3|-f（x）＜2a成立，求實數a的取值范圍．
  組卷：65引用：6難度：0.6

  解析