當(dāng)前位置：試卷中心 > 試卷詳情

2023-2024學(xué)年河北省承德市雙灤實(shí)驗(yàn)中學(xué)高二（上）開(kāi)學(xué)摸底數(shù)學(xué)試卷

發(fā)布：2024/8/8 8:0:9

1．下列敘述正確的是（　　）

A．互斥事件一定不是對(duì)立事件，但是對(duì)立事件一定是互斥事件

B．若事件A發(fā)生的概率為P（A），則0≤P（A）≤1

C．頻率是穩(wěn)定的，概率是隨機(jī)的

D．5張獎(jiǎng)券中有一張有獎(jiǎng)，甲先抽，乙后抽，那么乙比甲抽到有獎(jiǎng)獎(jiǎng)券的可能性小

組卷：401引用：4難度：0.7

A．這種抽樣方法是一種分層抽樣

B．這種抽樣方法是一種系統(tǒng)抽樣

C．這五名男生成績(jī)的方差大于這五名女生成績(jī)的方差

D．該班男生成績(jī)的平均數(shù)大于該班女生成績(jī)的平均數(shù)

組卷：843引用：50難度：0.9

3．已知m,n是兩條直線(xiàn)，α，β是兩個(gè)平面．給出下列命題：①若m⊥α，m⊥n,則n∥α；②若m⊥β，n⊥β，則n∥m；③若m⊥α，m⊥β，則α∥β；④若α∥β，m?α，n?β，則n∥m；⑤α⊥β，m?α，n?β，則m⊥n,則命題正確的個(gè)數(shù)為（　　）
A．1 B．2 C．3 D．4
組卷：402引用：6難度：0.7
解析
4．已知復(fù)數(shù)
z
=
（
3
i
-
1
）
（
1
-
i
）
i
2019
（i為虛數(shù)單位），則下列說(shuō)法正確的是（　　）
A．z的虛部為4
B．復(fù)數(shù)z在復(fù)平面內(nèi)對(duì)應(yīng)的點(diǎn)位于第三象限
C．z的共軛復(fù)數(shù)
z
=
4
-
2
i
D．
|
z
|
=
2
5
組卷：158引用：10難度：0.8
解析
5．在三棱錐P-ABC中，PA⊥平面ABC，PA=6，BC=3，
∠
CAB
=
π
6
，則三棱錐P-ABC的外接球半徑為（　　）
A．3 B．
2
3
C．
3
2
D．6
組卷：828引用：8難度：0.7
解析
6．在∠A=90°的等腰直角△ABC中，E為AB的中點(diǎn)，F(xiàn)為BC的中點(diǎn)，
BC
=
λ
AF
+μ
CE
，則λ=（　　）
A．-
2
3
B．
-
3
2
C．
-
4
3
D．-1
組卷：391引用：2難度：0.7
解析
7．將等腰直角三角形ABC沿斜邊上的高線(xiàn)AD折成60°的二面角，則折后的直線(xiàn)BC與平面ABD所成角的正弦值（　　）
A．
1
2
B．
3
3
C．
2
2
D．
3
2
組卷：20引用：3難度：0.6
解析

21．在△ABC中，a,b,c分別為內(nèi)角A，B，C所對(duì)的邊長(zhǎng)，
asin
A
+
bsin
B
-
csin
C
sin
B
sin
C
=
2
3
3
a
．
（1）求角C；
（2）若△ABC的中線(xiàn)CD的長(zhǎng)為
3
，求△ABC的面積的最大值．
組卷：21引用：2難度：0.5
解析
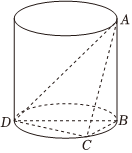22．如圖所示，已知圓柱的側(cè)面展開(kāi)圖的面積為6π，底面直徑BD=2，C為底面上異于B，D的點(diǎn)，且∠BDC=30°．求：
（1）二面角A-CD-B的余弦值；
（2）點(diǎn)B到平面ACD的距離．
組卷：10引用：4難度：0.5
解析