2023-2024學年廣東省佛山市南海區九江中學高二(上)期中數學試卷
發布:2024/10/20 16:0:2
一.選擇題
-
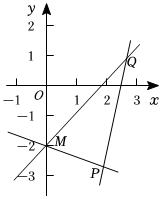 1.如圖,已知直線PM、QP、QM的斜率分別為k1、k2、k3,則k1、k2、k3的大小關系為( )
1.如圖,已知直線PM、QP、QM的斜率分別為k1、k2、k3,則k1、k2、k3的大小關系為( )A.k1<k3<k2 B.k1<k2<k3 C.k2<k1<k3 D.k3<k2<k1 組卷:297引用:7難度:0.7 -
2.在一個不透明的袋中有4個紅球和n個黑球,現從袋中有放回地隨機摸出2個球,已知取出的球中至少有一個紅球的概率為
,則n=( )89A.1 B.2 C.3 D.4 組卷:206引用:5難度:0.7 -
 3.如圖,在空間四邊形OABC中,,OA=a,OB=b,點M滿足OC=c,點N為BC的中點,則OM=2MA=( )MN
3.如圖,在空間四邊形OABC中,,OA=a,OB=b,點M滿足OC=c,點N為BC的中點,則OM=2MA=( )MNA. 12a-23b+12cB. -23a+12b+12cC. 12a+12b-12cD. 23a+b-12c組卷:148引用:8難度:0.7 -
4.已知方程
表示的曲線是橢圓,則實數m的取值范圍是( )x22-m+y2m+1=1A.(-1,2) B. (-1,12)∪(12,2)C. (-1,12)D. (12,2)組卷:2321引用:7難度:0.8 -
5.若兩異面直線l1與l2的方向向量分別是
=(1,0,-1),n1=(0,-1,1),則直線l1與l2的夾角為( )n2A.30° B.60° C.120° D.150° 組卷:806引用:12難度:0.8 -
6.在圓M:x2+y2-4x+2y-4=0內,過點O(0,0)的最長弦和最短弦分別是AC和BD,則四邊形ABCD的面積為( )
A.24 B.12 C.10 D.8 組卷:148引用:6難度:0.6 -
7.拋擲一枚質地均勻的骰子兩次,設“第一次向上的點數是2”為事件A,“第二次向上的點數是奇數”為事件B,“兩次向上的點數之和能被3整除”為事件C,則下列說法正確的是( )
A.事件A與事件B互為對立事件 B. P(C)=16C. P(BC)=16D.事件B與事件C相互不獨立 組卷:173引用:6難度:0.8
四.解答題
-
21.已知圓C經過點M(-2,0),N(0,2)兩點,且圓心在直線x-y=0上.
(1)求圓C的方程;
(2)已知l1、l2是過點(0,1)且互相垂直的兩條直線,且l1與C交于A,B兩點,l2于C交于P、Q兩點,求四邊形APBQ面積的最大值.組卷:152引用:3難度:0.7 -
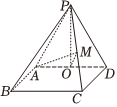 22.如圖,在四棱錐P-ABCD中,底面ABCD是邊長為2的菱形,∠ADC=60°,△PAD為正三角形,O為AD的中點,且平面PAD⊥平面ABCD,M是線段PC上的點.
22.如圖,在四棱錐P-ABCD中,底面ABCD是邊長為2的菱形,∠ADC=60°,△PAD為正三角形,O為AD的中點,且平面PAD⊥平面ABCD,M是線段PC上的點.
(1)求證:OM⊥BC;
(2)是否存在點M,使得直線AM與平面PAB的夾角的正弦值為,若存在;求出此時1010的值;若不存在,請說明理由.PMPC組卷:39引用:1難度:0.5


