2022-2023學年湖南省長沙市明德教育集團七年級（下）期中數學試卷

一、選擇題（每題3分，在下列各題的四個選項中，只有一個是符合題意的，請在答題卡中填涂符合隨意的選項，本大題共10個小題，共30分）

• 1．下列選項中，最小的數是（　　）

  A．1

  B．-3

  C．0

  D．-π
  組卷：61引用：2難度：0.9

  解析

• 2．下列各圖中，∠1與∠2是對頂角的是（　　）

  A．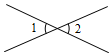

  B．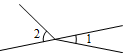

  C．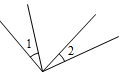

  D．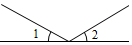
  組卷：1768引用：23難度：0.9

  解析

• 3．在平面直角坐標系中，點A（5，3）到x軸距離為（　　）

  A．4

  B．-4

  C．3

  D．-3
  組卷：197引用：3難度：0.6

  解析

• 4．下列語句中，真命題是（　　）

  A．-3是9的平方根

  B．從直線外一點到這條直線的垂線段，叫做這點到這條直線的距離

  C．若a2=b2，則a=b

  D．相等的兩個角是對頂角
  組卷：90引用：2難度：0.7

  解析

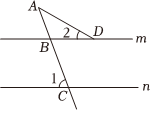• 5．如圖，直線m∥n,∠1=70°，∠2=30°，則∠A等于（　　）

  A．30°

  B．35°

  C．40°

  D．50°
  組卷：7374引用：60難度：0.9

  解析

• 6．在下列實數

  3

  ，0.31，

  π

  3

  ，

  1

  7

  ，

  9

  ，1.212212221…（每兩個1之間依次多一個2）中，無理數的個數為（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：239引用：4難度：0.8

  解析

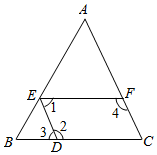• 7．如圖，能判定DE∥AC的條件是（　　）

  A．∠3=∠C

  B．∠1=∠3

  C．∠2=∠4

  D．∠1+∠2=180°
  組卷：886引用：13難度：0.9

  解析

• 8．由方程組

  x + m = 4

  y - 3 = m

  可得出x與y的關系是（　　）

  A．x+y=1

  B．x+y=-1

  C．x+y=7

  D．x+y=-7
  組卷：3250引用：45難度：0.9

  解析

三、解答題（本大題共9個小題，第17、18、19題每小題6分，第20、21題每小題6分，第22、23題每小題6分，第24、25題每小題6分，共72分）

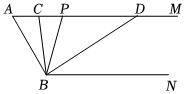• 24．如圖，已知AM∥BN，點P是射線AM上一動點（與點A不重合），BC，BD分別平分∠ABP和∠PBN，分別交射線AM于點C，D．
  （1）若∠A=40°，則∠CBD=

  ；（直接寫出答案）
  （2）當點P運動時，∠APB與∠ADB之間的數量關系是否隨之發生改變？若不變化，請寫出它們之間的關系，并說明理由；若變化，請寫出變化規律；
  （3）當∠A=2∠ABC，4∠BCM=3∠BDC，求∠A的度數．
  組卷：454引用：2難度：0.5

  解析

• 25．在平面直角坐標系中，對于給定的兩點P，Q，若存在點M，使得三角形MPQ的面積等于k,則稱點M為線段PQ的“k系數面積點”，記作S（M，△MPQ）=k；當k=1，則稱點M為線段PQ的“單位面積點”．（三角形MPQ我們一般記作“△MPQ”）如圖，在平面直角坐標系中，點P的坐標為（-1，0）．
  
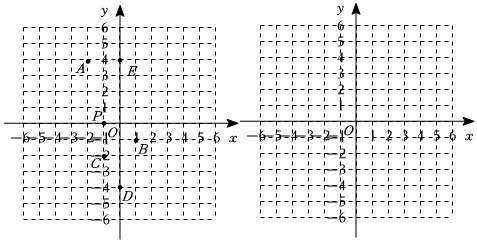
  （1）在A（-2，4），B（1-1），C（-1，-2），D（0，-4）這四個點中，是線段OP的“2系數面積點”有

  ．
  （2）已知點E的坐標為（0，4），點O為坐標原點，若x軸上存在一動點F（m,0），滿足S（F，△FPE）=4，求m的值；
  （3）已知點Q的坐標為（-1，2），點M在第二象限內且點M的縱坐標為3，點N在直線PQ的右側，點M、N是線段PQ的兩個“單位面積點”，當△OMN是△NPQ面積的

  5

  2

  倍時，求點N的坐標．
  組卷：300引用：2難度：0.3

  解析