當前位置：試卷中心 > 試卷詳情

2020-2021學年安徽省淮南市壽縣一中高一（下）入學數學試卷

發布：2024/11/5 9:0:2

一、選擇題：共12小題，每小題5分，滿分60分.在每小題給出的四個選項中，只有一項是符合題目要求的.

1．已知全集為U，集合A={-2，0，1，2}，B={x|-2≤x≤0}，集合A和集合B的韋恩圖如圖所示，則圖中陰影部分可表示為（　　）
A．（-2，0） B．[-1，0] C．{-1，0} D．{-2，1，2}
組卷：167引用：9難度：0.9
解析
2．是
a
=
（
1
，-
2
）
，
b
=
（
-
3
，
4
）
，
c
=
（
3
，
2
）
，則
（
a
+
2
b
）
?
c
=（　　）
A．12 B．0 C．-3 D．-11
組卷：183引用：4難度：0.8
解析
3．已知角α頂點在原點，始邊與x軸正半軸重合，點
P
（
-
1
，-
3
）
在終邊上，則
sin
（
α
+
π
3
）
=（　　）
A．0 B．
-
1
2
C．
-
3
2
D．-1
組卷：223引用：5難度：0.9
解析
4．已知
e
1
，
e
2
是兩個不共線的向量，若
AB
=
2
e
1
-
8
e
2
，
CB
=
e
1
+
3
e
2
，
CD
=
2
e
1
-
e
2
，則（　　）
A．點A，B，D共線 B．點A，C，D共線
C．點A，B，C共線 D．點B，C，D共線
組卷：23引用：1難度：0.8
解析
5．設向量
a
，
b
滿足|
a
|=|
b
|=1及|3
a
-2
b
|=
7
，則
a
，
b
的夾角為（　　）
A．
π
3
B．
π
6
C．
π
4
D．
2
π
3
組卷：32引用：1難度：0.8
解析
6．若抽氣機每次可抽出容器內空氣的60%，要使容器內的空氣少于原來的0.1%，則至少要抽（參考數據：lg2≈0.3010）（　　）
A．6次 B．7次 C．8次 D．9次
組卷：18引用：1難度：0.8
解析
7．等腰三角形的底和腰之比為黃金分割比的三角形稱為黃金三角形，它是最美三角形．例如，正五角星是有5個最美三角形和一個正五邊形組成，每一個最美三角形的頂角都是36°，如圖所示，在黃金三角形ABC中，
BC
AB
=
5
-
1
2
，根據這些信息，可求得cos144°的值為（　　）
A．
1
-
5
4
B．
-
5
-
1
2
C．
-
1
+
5
4
D．
-
3
+
5
8
組卷：7引用：1難度：0.8
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題：共6小題，滿分70分.解答應寫出文字說明，證明過程和解題步驟.

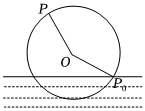21．如圖一個水輪的半徑為4m,水輪圓心O距離水面2m,已知水輪每分鐘轉動5圈（按逆時針轉動），當水輪上點P從水中浮現（圖中點P₀）時開始計算時間．
（1）已知點P距離水面的高度H（m）與時間t（s）滿足函數模型
H
=
A
sin
（
ωt
+
φ
）
+
h
（
A
＞
0
，
ω
＞
0
，-
π
2
＜
φ
＜
π
2
）
，試求H的表達式；
（2）求點P第一次到達最高點需要多長時間？
組卷：15引用：1難度：0.7
解析
22．已知函數
f
（
x
）
=
x
+
t
x
，t∈R．
（Ⅰ）當t=2時，寫出f（x）的單調遞減區間（不必證明），并求f（x）的值域；
（Ⅱ）設函數
g
（
x
）
=
-
4
cos
（
x
+
π
3
）
，若對任意x₁∈[1，2]，總有x₂∈[0，π]，使得f（x₁）=g（x₂），求實數t的取值范圍．
組卷：84引用：6難度：0.3
解析