2023年海南省瓊海市高考數學模擬試卷
發布:2024/11/16 14:0:2
一、選擇題:本題共8小題,每小題5分,共40分.在每小題給出的四個選項中,只有一項是符合題目要求的.
-
1.
=( )(1+3i)2A. 2+23iB. 2-23iC. -2+23iD. -2-23i組卷:43引用:2難度:0.8 -
2.已知集合A={x|a<x<a2+1,a∈Z},B={x|2<x<6},若A∩B=A,則a=( )
A.1 B.2 C.3 D.4 組卷:53引用:3難度:0.8 -
3.
=( )(3727)7+3A.9 B. 19C.3 D. 39組卷:334引用:4難度:0.7 -
4.如圖①,這是一個小正方體的側面展開圖,將小正方體從如圖②所示的位置依次翻到第1格、第2格、第3格、第4格、第5格、第6格,這時小正方體正面朝上的圖案是( )
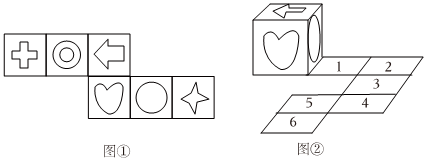
A. 
B. 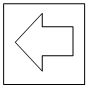
C. 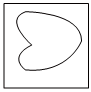
D.  組卷:22引用:6難度:0.8
組卷:22引用:6難度:0.8 -
5.小方計劃從4月1日開始存儲零錢,4月1日到4月4日每天都存儲1元,從4月5日開始,每天存儲的零錢比昨天多1元,則小方存錢203天(4月1日為第1天)的儲蓄總額為( )
A.19903元 B.19913元 C.20103元 D.20113元 組卷:89引用:7難度:0.8 -
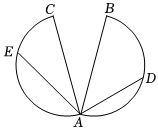 6.如圖,已知AB=AC,∠BAC=,分別以AB,AC為直徑作半圓弧,D是半圓弧的中點,E為半圓弧上靠近點C的三等分點,則向量π6在向量AE上的投影向量為( )AD
6.如圖,已知AB=AC,∠BAC=,分別以AB,AC為直徑作半圓弧,D是半圓弧的中點,E為半圓弧上靠近點C的三等分點,則向量π6在向量AE上的投影向量為( )ADA. 3-38ADB. 2-38ADC. 3-34ADD. 2-34AD組卷:52引用:4難度:0.6 -
7.當x,y∈(0,+∞)時,
恒成立,則m的取值范圍是( )4x4+17x2y+4y2x4+2x2y+y2<m4A.(25,+∞) B.(26,+∞) C. (994,+∞)D.(27,+∞) 組卷:132引用:4難度:0.5
四、解答題:本題共6小題,共70分.解答應寫出文字說明、證明過程或演算步驟.
-
21.已知M,N分別為橢圓
的左,右頂點,F為其右焦點,|FM|=3|FN|,且點E:x2a2+y2b2=1(a>b>0)在橢圓E上.P(1,32)
(1)求橢圓E的標準方程;
(2)若過F的直線l與橢圓E交于A,B兩點,且l與以MN為直徑的圓交于C,D兩點,證明:為定值.12|AB|+|CD|24組卷:147引用:5難度:0.6 -
22.已知函數
.f(x)=exx+lnx
(1)求曲線f(x)在x=1處的切線方程;
(2)寫出一個適當的正整數a,使得恒成立,并證明.f(x)>(2a+1)lnx+1x組卷:56引用:4難度:0.5


