2022-2023學年遼寧省朝陽市建平實驗中學高一（上）期中數(shù)學試卷

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．設集合M={x|0＜x＜4}，N={x|

  1

  3

  ≤x≤5}，則（?_RM）∩N=（　　）

  A． { x | 0 ＜ x ≤ 1 3 }

  B． { x | 1 3 ≤ x ＜ 4 }

  C．{x|0＜x≤5}

  D．{x|4≤x≤5}
  組卷：58引用：2難度：0.8

  解析

• 2．已知命題p：?x∈R，x²+2x＜0，則￢p為（　　）

  A．?x∈R，x2+2x≤0	B．?x∈R，x2+2x＞0
  C．?x∈R，x2+2x≥0	D．?x∈R，x2+2x＜0
  組卷：148引用：5難度：0.9

  解析

• 3．函數(shù)

  f

  （

  x

  ）

  =

  （

  x

  -

  1

  ）

  0

  +

  1

  x

  +

  2

  的定義域為（　　）

  A．（1，+∞）	B．（-2，+∞）
  C．（-2，1）∪（1，+∞）	D．R
  組卷：545引用：4難度：0.9

  解析

• 4．“x＞1”是“x²＞1”的（　　）

  A．必要不充分條件	B．充分不必要條件
  C．充要條件	D．既不充分也不必要條件
  組卷：99引用：13難度：0.8

  解析

• 5．中文“函數(shù)（function）”一詞，最早是由近代數(shù)學家李善蘭翻譯出來的，之所以這么翻譯，他給出的原因是“凡此變數(shù)中函彼變數(shù)者，則此為彼之函數(shù)”，即函數(shù)指一個量隨著另一個量的變化而變化，下列四組函數(shù)，表示同一函數(shù)的是（　　）

  A．f（x）=1，g（x）=x0

  B．f（x）=x（x∈R）與g（x）=x（x∈Z）

  C．f（x）=|x|與 g （ x ） = x , x ≥ 0 - x , x ＜ 0

  D． f （ x ） = x + 2 ? x - 2 ， g （ x ） = x 2 - 4
  組卷：318引用：4難度：0.7

  解析

• 6．函數(shù)y=|x-2|?x的圖象大致形狀是（　　）

  A．

  B．

  C．

  D．
  組卷：38引用：2難度：0.7

  解析

• 7．已知f（x）是定義在R上的偶函數(shù)，當x＜0時，f（x）=x²-3x-1，則當x＞0時，f（x）=（　　）

  A．-x2-3x+1

  B．x2+3x-1

  C．-x2+3x+1

  D．x2-3x-1
  組卷：121引用：1難度：0.7

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

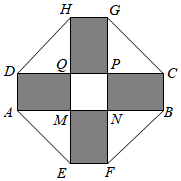• 21．如圖，徐州某居民小區(qū)要建一座八邊形的展館區(qū)，它的主體造型的平面圖是由兩個相同的矩形ABCD和EFGH構成的面積為200m²的十字形地域，計劃在正方形MNPQ上建一座花壇，造價為4200元/m²；在四個相同的矩形（圖中陰影部分）上鋪花崗巖地坪，造價為210元/m²；再在四個空角（圖中四個三角形）鋪草坪，造價為80元/m²．
  （1）設總造價為S（單位：元），AD長為x（單位：m），求出S關于x的函數(shù)關系式；
  （2）當AD長取何值時，總造價S最小，并求這個最小值．
  組卷：189引用：15難度：0.7

  解析

• 22．設函數(shù)f（x）=|ax|+（x+a）（x-a）（a∈R）．
  （1）當a=1時，在平面直角坐標系中作出函數(shù)f（x）的大致圖象，并寫出f（x）的單調區(qū)間（無需證明）；
  （2）若x∈[a,a+1]，求函數(shù)f（x）的最小值．
  組卷：31引用：2難度：0.4

  解析