當前位置：試卷中心 > 試卷詳情

2022-2023學年浙江大學附中丁蘭校區高一（上）期末數學試卷

發布：2024/11/10 21:0:1

1．若集合
M
=
{
x
|
x
＜
4
}
，N={x|3x≥1}，則M∩N=（　　）
A．[0，2） B．
[
1
3
，
2
）
C．[3，16） D．
[
1
3
，
16
）
組卷：75引用：2難度：0.8
解析
2．下列函數中，定義域為（0，+∞）的是（　　）
A．f（x）=e^x B．f（x）=lnx C．
f
（
x
）
=
1
x
D．f（x）=|x|
組卷：176引用：3難度：0.7
解析
3．設x∈R，則“sinx=1”是“cosx=0”的（　　）
A．充分不必要條件 B．必要不充分條件
C．充分必要條件 D．既不充分也不必要條件
組卷：2860引用：38難度：0.8
解析
4．若函數f（x）=
-
x
2
，
x
≥
0
2
x
，
x
＜
0
，則函數f（x）的值域為（　　）
A．[0，1） B．（-∞，0]
C．（-∞，0）∪（0，1） D．（-∞，1）
組卷：1653引用：6難度：0.8
解析
5．函數
f
（
x
）
=
xlg
|
x
-
1
|
|
x
|
的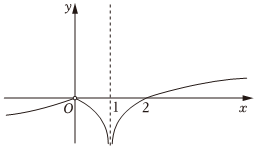圖象大致是（　　）
A． B．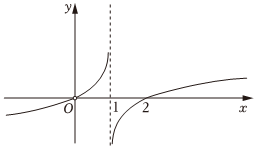
C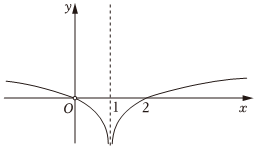． D．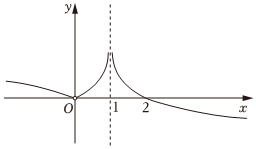
組卷：210引用：2難度：0.7
解析
6．設tanα，tanβ是方程x²-3x+2=0的兩個根，則tan（α+β）的值為（　　）
A．-3 B．-1 C．1 D．3
組卷：2634引用：49難度：0.7
解析
7．設f（x）是定義域為R的偶函數，且在（0，+∞）單調遞減，則（　　）
A．f（log₃
1
4
）＞f（
2
-
3
2
）＞f（
2
-
2
3
）
B．f（log₃
1
4
）＞f（
2
-
2
3
）＞f（
2
-
3
2
）
C．f（
2
-
3
2
）＞f（
2
-
2
3
）＞f（log₃
1
4
）
D．f（
2
-
2
3
）＞f（
2
-
3
2
）＞f（log₃
1
4
）
組卷：11024引用：40難度：0.5
解析

A．充分不必要條件	B．必要不充分條件
C．充分必要條件	D．既不充分也不必要條件

A．[0，1）	B．（-∞，0]
C．（-∞，0）∪（0，1）	D．（-∞，1）

A．	B．
C．	D．

1．若集合M={x|x＜4}，N={x|3x≥1}，則M∩N=（ ）