2023年江蘇省蘇州五中高考數(shù)學(xué)適應(yīng)性試卷（4月份）

一、單選題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．復(fù)數(shù)

  z

  =

  1

  1

  -

  i

  （i是虛數(shù)單位）在復(fù)平面上對應(yīng)的點位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：63引用：10難度：0.9

  解析

• 2．函數(shù)

  f

  （

  x

  ）

  =

  1

  2

  x

  -

  sinx

  的圖象可能是（　　）

  A．

  B．

  C．

  D．
  組卷：87引用：1難度：0.8

  解析

• 3．已知函數(shù)

  f

  （

  x

  ）

  =

  | lnx | ， x ＞ 0

  x 2 + 2 x - 1 ， x ≤ 0

  ，若方程f（x）=ax-1有且僅有三個實數(shù)解，則實數(shù)a的取值范圍為（　　）

  A．0＜a＜1

  B．0＜a＜2

  C．a(chǎn)＞1

  D．a(chǎn)＞2
  組卷：499引用：5難度：0.7

  解析

• 4．如圖，點A，B，C，M，N為正方體的頂點或所在棱的中點，則下列各圖中，不滿足直線MN∥平面ABC的是（　　）

  A．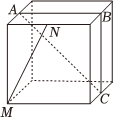

  B．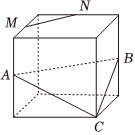

  C．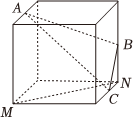

  D．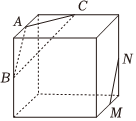
  組卷：939引用：12難度：0.5

  解析

• 5．我國油紙傘的制作工藝巧妙．如圖（1），傘不管是張開還是收攏，傘柄AP始終平分同一平面內(nèi)兩條傘骨所成的角∠BAC，且AB=AC，從而保證傘圈D能夠沿著傘柄滑動．如圖（2），傘完全收攏時，傘圈D已滑到D'的位置，且A，B，D'三點共線，AD'=40cm,B為AD'的中點，當(dāng)傘從完全張開到完全收攏，傘圈D沿著傘柄向下滑動的距離為24cm,則當(dāng)傘完全張開時，∠BAC的余弦值是（　　）
  

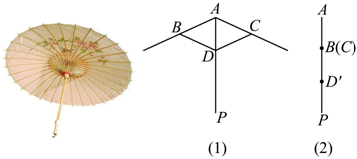
  A． - 17 25

  B． - 4 21 25

  C． - 3 5

  D． - 8 25
  組卷：656引用：20難度：0.6

  解析

• 6．A、B兩組各3人獨(dú)立的破譯某密碼，A組每個人譯出該密碼的概率均為p₁，B組每個人譯出該密碼的概率均為p₂，記A、B兩組中譯出密碼的人數(shù)分別為X、Y，且

  1

  2

  ＜

  p

  1

  ＜

  p

  2

  ＜

  1

  ，則（　　）

  A．E（X）＜E（Y），D（X）＜D（Y）	B．E（X）＜E（Y），D（X）＞D（Y）
  C．E（X）＞E（Y），D（X）＜D（Y）	D．E（X）＞E（Y），D（X）＞D（Y）
  組卷：215引用：3難度：0.6

  解析

• 7．過拋物線y²=4x的焦點作兩條互相垂直的弦AB，CD，則四邊形ACBD面積的最小值為（　　）

  A．8

  B．16

  C．32

  D．64
  組卷：210引用：4難度：0.5

  解析

四、解答題：本題共6小題，共70分.解答時應(yīng)寫出必要的文字說明、證明過程或演算步驟.

• 21．已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的離心率為

  3

  2

  ，左，右頂點分別為A，B，點P，Q為橢圓上異于A，B的兩點，△PAB面積的最大值為2．
  （1）求橢圓C的方程；
  （2）設(shè)直線AP，QB的斜率分別為k₁，k₂，且3k₁=5k₂．
  （i）求證：直線PQ經(jīng)過定點．
  （ii）設(shè)△PQB和△PQA的面積分別為S₁，S₂，求|S₁-S₂|的最大值．
  組卷：904引用：6難度：0.2

  解析

• 22．已知函數(shù)f（x）=e^x-

  a

  x

  （a∈R）．
  （1）討論函數(shù)f（x）零點個數(shù)；
  （2）若|f（x）|＞alnx-a恒成立，求a的取值范圍．
  組卷：443引用：6難度：0.5

  解析