2022年江蘇省南京第五高級中學高考數學一模試卷

一、單項選擇題：本大題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．已知復數z滿足（1+i）z=（1-i）²，則z的實部為（　　）

  A．1

  B．-1

  C．2

  D．-2
  組卷：164引用：2難度：0.8

  解析

• 2．已知集合A={x∈N|x²-2x-3≤0}，b={x|y=log₂（3-x）}，則A∪B=（　　）

  A．（-∞，3]

  B．{0，1，2，3}

  C．{0，1，2}

  D．R
  組卷：151引用：8難度：0.8

  解析

• 3．函數

  f

  （

  x

  ）

  =

  x

  -

  2

  x

  -

  lnx

  的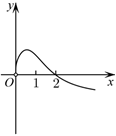圖象大致為（　　）

  A．

  B．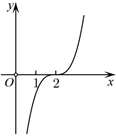

  C．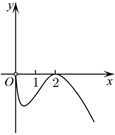

  D．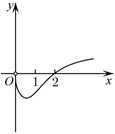
  組卷：258引用：4難度：0.8

  解析

• 4．假定生男孩和生女孩是等可能的，現考慮有3個小孩的家庭，隨機選擇一個家庭，則下列說法正確的是（　　）

  A．事件“該家庭3個小孩中至少有1個女孩”和事件“該家庭3個小孩中至少有1個男孩”是互斥事件

  B．事件“該家庭3個孩子都是男孩”和事件“該家庭3個孩子都是女孩”是對立事件

  C．該家庭3個小孩中只有1個男孩的概率為 1 8

  D．當已知該家庭3個小孩中有男孩的條件下，3個小孩中至少有2個男孩的概率為 4 7
  組卷：652引用：3難度：0.7

  解析

• 5．區塊鏈作為一種新型的技術，已經被應用于許多領域．在區塊鏈技術中，某個密碼的長度設定為512B，則
  密碼一共有2⁵¹²種可能，為了破解該密碼，最壞的情況需要進行2⁵¹²次運算．現在有一臺計算機，每秒能進行1.25×10¹³次運算，那么在最壞的情況下，這臺計算機破譯該密碼所需時間大約為（　　）
  （參考數據：lg2≈0.3，

  10

  ≈

  3

  .

  16

  ）

  A．6.32×10141s	B．6.32×10140s
  C．3.16×10141s	D．3.16×10140s
  組卷：299引用：11難度：0.5

  解析

• 6．已知sin（

  π

  4

  -α）=

  3

  5

  ，則

  sinα

  1

  -

  tanα

  的值為（　　）

  A．- 7 2 60

  B． 7 2 60

  C．- 7 2 30

  D． 7 2 30
  組卷：406引用：8難度：0.7

  解析

• 7．已知橢圓

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的左、右焦點分別為F₁，F₂，點A在橢圓上且位于第二象限，滿足

  A

  F

  1

  ?

  A

  F

  2

  =

  0

  ，∠AF₁F₂的平分線與AF₂相交于點B，若

  AB

  =

  3

  8

  A

  F

  2

  ，則橢圓的離心率為（　　）

  A． 2 7

  B． 3 7

  C． 4 7

  D． 5 7
  組卷：1045引用：3難度：0.6

  解析

四、解答題：本題共6小題，共70分。解答應寫出必要的文字說明、證明過程或演算步驟。

• 21．圖1是由矩形ACC₁A₁、等邊△ABC和平行四邊形ABB₁A₂組成的一個平面圖形，其中AB=2，AA₁=AA₂=1，N為A₁C₁的中點．將其沿AC，AB折起使得AA₁與AA₂重合，連結B₁C₁，BN，如圖2．
  
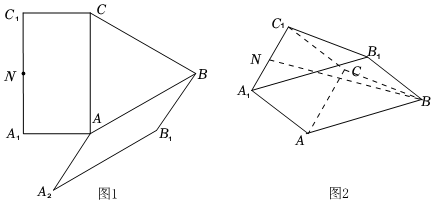
  （1）證明：在圖2中，AC⊥BN，且B，C，C₁，B₁四點共面；
  （2）在圖2中，若二面角A₁-AC-B的大小為θ，且

  tanθ

  =

  -

  1

  2

  ，求直線AB與平面BCC₁B₁所成角的正弦值．
  組卷：473引用：4難度：0.5

  解析

• 22．已知函數f（x）=

  2

  3

  x³-mx²+m²x（m∈R）的導函數為f′（x）．
  （1）若函數g（x）=f（x）-f′（x）存在極值，求m的取值范圍；
  （2）設函數h（x）=f′（e^x）+f′（lnx）（其中e為自然對數的底數），對任意m∈R，若關于x的不等式h（x）≥m²+k²在（0，+∞）上恒成立，求正整數k的取值集合．
  組卷：442引用：3難度：0.1

  解析