2010年六年級奧數題：染色問題（A）

一、解答題（共14小題，滿分0分）

• 1．某影院有31排，每排29個座位．某天放映了兩場電影，每個座位上都坐了一個觀眾．如果要求每個觀眾在看第二場電影時必須跟他（前、后、左、右）相鄰的某一觀眾交換座位，這樣能辦到嗎？為什么？
  組卷：35引用：2難度：0.9

  解析

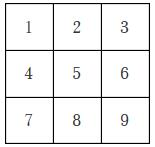• 2．如圖是一所房子的示意圖，圖中數字表示房間號碼，每間房子都與隔壁的房間相通．問能否從1號房間開始，不重復的走遍所有房間又回到1號房間？
  組卷：50引用：3難度：0.9

  解析

• 3．在一個正方形的果園里種有63棵果樹，加上右下角的一間小屋，整齊地排列成八行八列（見圖（a））．守園人從小屋出發經過每一棵樹，不重復也不遺漏（不許斜走），最后又回到小屋，行嗎？如果有80棵果樹，連小屋在內排成九行九列（圖（b））呢？
  組卷：40引用：4難度：0.5

  解析

• 4．一個8×8國際象棋（下圖）去掉對角上兩格后，是否可以用31個2×1的“骨牌”（形如）把象棋盤上的62個小格完全蓋住？
  組卷：21引用：1難度：0.5

  解析

一、解答題（共14小題，滿分0分）

• 13．8×8的國際象棋棋盤能不能被剪成7個2×2的正方形和9個4×1的長方形？如果可以，請給出一種剪法；如果不行，請說明理由．
  組卷：31引用：2難度：0.3

  解析

• 14．（表1）是由數字0，1交替構成的，（表2）是由（表1）中任選三種形式組成的圖形，并在每個小方格全部加1或減1，如此反復多次進行形成的，試問（表2）中的A格上的數字是多少？并說明理由．
  
  

  1	0	1	0	1	0	1	0
  0	1	0	1	0	1	0	1
  1	0	1	0	1	0	1	0
  0	1	0	1	0	1	0	0
  1	0	1	0	1	0	1	0
  0	1	0	1	0	1	0	1
  1	0	1	0	1	0	1	0
  0	1	0	1	0	1	0	1

  表（1）

  1	1	1	1	1	1	1	1
  1	1	1	1	1	1	1	1
  1	1	1	1	1	1	1	1
  1	1	1	1	1	1	1	1
  1	1	1	1	1	1	A	1
  1	1	1	1	1	1	1	1
  1	1	1	1	1	1	1	1
  1	1	1	1	1	1	1	1

  表（2）
  組卷：26引用：2難度：0.1

  解析