2022年廣東省東莞市石龍鎮中考數學一模試卷
發布:2024/12/13 11:30:2
一、選擇題(本大題共10個小題,每題3分,滿分30分.在下列每個小題給出的四個答案中有且只有一個正確答案,請將正確答案的字母代號在答題卡上涂黑,涂錯或不涂均為零分)
-
1.-2的絕對值是( )
A.2 B.- 12C. 12D.-2 組卷:106引用:2難度:0.7 -
2.剪紙藝術是最古老的中國民間藝術之一,先后入選中國國家級非物質文化遺產名錄和人類非物質文化遺產代表作名錄.魚與“余”同音,寓意生活富裕、年年有余,是剪紙藝術中很受喜愛的主題.以下關于魚的剪紙中,既是軸對稱圖形又是中心對稱圖形的是( )
A. 
B. 
C. 
D.  組卷:347引用:11難度:0.9
組卷:347引用:11難度:0.9 -
3.下列計算正確的是( )
A.m2?m3=m6 B.-(m-n)=-m+n C.m(m+n)=m2+n D.(m+n)2=m2+n2 組卷:635引用:16難度:0.7 -
4.實數a,b在數軸上的對應點的位置如圖所示,則下列結論中,正確的是( )
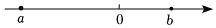
A.a>b B.a=b C.a<b D.a=-b 組卷:448引用:10難度:0.8 -
 5.如圖是某一水塘邊的警示牌,牌面是五邊形,這個五邊形的內角和是( )
5.如圖是某一水塘邊的警示牌,牌面是五邊形,這個五邊形的內角和是( )A.900° B.720° C.540° D.360° 組卷:627引用:12難度:0.7 -
 6.甲、乙兩種物質的溶解度y(g)與溫度t(℃)之間的對應關系如圖所示,則下列說法中,錯誤的是( )
6.甲、乙兩種物質的溶解度y(g)與溫度t(℃)之間的對應關系如圖所示,則下列說法中,錯誤的是( )A.甲、乙兩種物質的溶解度均隨著溫度的升高而增大 B.當溫度升高至t2℃時,甲的溶解度比乙的溶解度大 C.當溫度為0℃時,甲、乙的溶解度都小于20g D.當溫度為30℃時,甲、乙的溶解度相等 組卷:1354引用:23難度:0.8 -
7.下列命題不正確的是( )
A.經過直線外一點,有且只有一條直線與這條直線平行 B.負數的立方根是負數 C.對角線互相垂直的四邊形是菱形 D.五邊形的外角和是360° 組卷:568引用:6難度:0.6 -
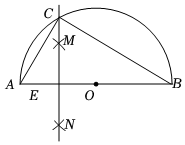 8.如圖,線段AB是半圓O的直徑.分別以點A和點O為圓心,大于的長為半徑作弧,兩弧交于M,N兩點,作直線MN,交半圓O于點C,交AB于點E,連接AC,BC,若AE=1,則BC的長是( )12AO
8.如圖,線段AB是半圓O的直徑.分別以點A和點O為圓心,大于的長為半徑作弧,兩弧交于M,N兩點,作直線MN,交半圓O于點C,交AB于點E,連接AC,BC,若AE=1,則BC的長是( )12AOA. 23B.4 C.6 D. 32組卷:861引用:13難度:0.7
三、解答題(本大題共8個題,滿分0分)
-
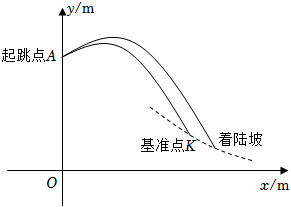 24.跳臺滑雪運動可分為助滑、起跳、飛行和落地四個階段,運動員起跳后飛行的路線是拋物線的一部分(如圖中實線部分所示),落地點在著陸坡(如圖中虛線部分所示)上,著陸坡上的基準點K為飛行距離計分的參照點,落地點超過K點越遠,飛行距離分越高.2022年北京冬奧會跳臺滑雪標準臺的起跳臺的高度OA為66m,基準點K到起跳臺的水平距離為75m,高度為h m(h為定值).設運動員從起跳點A起跳后的高度y(m)與水平距離x(m)之間的函數關系為y=ax2+bx+c(a≠0).
24.跳臺滑雪運動可分為助滑、起跳、飛行和落地四個階段,運動員起跳后飛行的路線是拋物線的一部分(如圖中實線部分所示),落地點在著陸坡(如圖中虛線部分所示)上,著陸坡上的基準點K為飛行距離計分的參照點,落地點超過K點越遠,飛行距離分越高.2022年北京冬奧會跳臺滑雪標準臺的起跳臺的高度OA為66m,基準點K到起跳臺的水平距離為75m,高度為h m(h為定值).設運動員從起跳點A起跳后的高度y(m)與水平距離x(m)之間的函數關系為y=ax2+bx+c(a≠0).
(1)c的值為 ;
(2)①若運動員落地點恰好到達K點,且此時a=-,b=150,求基準點K的高度h;910
②若a=-時,運動員落地點要超過K點,則b的取值范圍為 ;150
(3)若運動員飛行的水平距離為25m時,恰好達到最大高度76m,試判斷他的落地點能否超過K點,并說明理由.組卷:3757引用:21難度:0.4 -
25.綜合與實踐
問題提出
某興趣小組在一次綜合與實踐活動中提出這樣一個問題:將足夠大的直角三角板PEF(∠P=90°,∠F=60°)的一個頂點放在正方形中心O處,并繞點O逆時針旋轉,探究直角三角板PEF與正方形ABCD重疊部分的面積變化情況(已知正方形邊長為2).
操作發現
(1)如圖1,若將三角板的頂點P放在點O處,在旋轉過程中,當OF與OB重合時,重疊部分的面積為 ;當OF與BC垂直時,重疊部分的面積為 ;一般地,若正方形面積為S,在旋轉過程中,重疊部分的面積S1與S的關系為 ;
類比探究
(2)若將三角板的頂點F放在點O處,在旋轉過程中,OE,OP分別與正方形的邊相交于點M,N.
①如圖2,當BM=CN時,試判斷重疊部分△OMN的形狀,并說明理由;
②如圖3,當CM=CN時,求重疊部分四邊形OMCN的面積(結果保留根號:tan15°≈2-√3);
拓展應用
(3)若將任意一個銳角的頂點放在正方形中心O處,該銳角記為∠GOH(設∠GOH=α),將∠GOH繞點O逆時針旋轉,在旋轉過程中,∠GOH的兩邊與正方形ABCD的邊所圍成的圖形的面積為S2,請直接寫出S2的最小值與最大值(分別用含α的式子表示).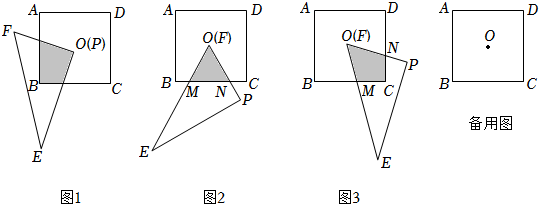 組卷:1822引用:4難度:0.1
組卷:1822引用:4難度:0.1


