2022年陜西省高考數(shù)學(xué)質(zhì)檢試卷（理科）（二）

一、選擇題：本題共12小題，每小題5分，共60分．在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的．

• 1．已知集合

  A

  =

  {

  x

  |

  x

  2

  -

  2

  x

  -

  8

  ≤

  0

  }

  ，

  B

  =

  {

  x

  |

  x

  -

  2

  x

  +

  3

  ≤

  0

  }

  ，則A∪B=（　　）

  A．{x|-4≤x≤2}	B．{x|-4≤x≤2且x≠-3}
  C．{x|-3≤x≤4}	D．{x|-3＜x≤4}
  組卷：190引用：5難度：0.8

  解析

• 2．已知復(fù)數(shù)z滿足（1+2i）z=5

  z

  -10i,則|z|=（　　）

  A． 2

  B．2

  C． 5

  D． 2 2
  組卷：162引用：2難度：0.7

  解析

• 3．命題p：?x∈[1，2]，2^x≥3，命題q：?x₀∈[1，2]，log₂x₀≥1，則下列命題為真命題的是（　　）

  A．p∧q

  B．（￢p）∧（￢q）

  C．p∨q

  D．p∨（￢q）
  組卷：129引用：3難度：0.7

  解析

• 4．若（1+mx²）（1+x）⁴的展開式中x³的系數(shù)為12，則實(shí)數(shù)m=（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：258引用：2難度：0.8

  解析

• 5．已知f（x）是R上的奇函數(shù)，當(dāng)x＜0時(shí)，f（x）=-e^-3x，則f（ln2）=（　　）

  A．e8

  B．8

  C．6

  D．ln2
  組卷：108引用：1難度：0.7

  解析

• 6．把函數(shù)f（x）=cos²x-sin²x的圖象向左平移

  π

  12

  個(gè)單位長(zhǎng)度得到函數(shù)g（x）的圖象，若g（x）在[0，a]上是減函數(shù)，則實(shí)數(shù)a的最大值為（　　）

  A． 5 π 12

  B． π 3

  C． π 6

  D． π 12
  組卷：93引用：3難度：0.6

  解析

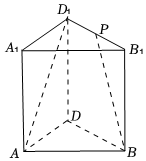• 7．如圖，在直三棱柱ABD-A₁B₁D₁中，AB=AD=AA₁，∠ABD=45°，P為B₁D₁的中點(diǎn)，則直線PB與AD₁所成的角為（　　）

  A．30°

  B．45°

  C．60°

  D．90°
  組卷：758引用：10難度：0.6

  解析

（二）選考題：共10分．請(qǐng)考生在第22，23題中任選一題作答，如果多做，則按所做的第一題計(jì)分，作答時(shí)，請(qǐng)用2B鉛筆在答題卡上將所選題號(hào)后的方框涂黑．[選修4-4：坐標(biāo)系與參數(shù)方程]（10分）

• 22．在直角坐標(biāo)系xOy中，直線l的參數(shù)方程為

  x = 3 + 3 t

  y = 3 + t

  （t是參數(shù)）．以O(shè)為極點(diǎn)，x軸正半軸為極軸建立極坐標(biāo)系，曲線C的極坐標(biāo)方程為ρ²+5ρ²sin²θ-36=0．
  （Ⅰ）求l的極坐標(biāo)方程和C的直角坐標(biāo)方程；
  （Ⅱ）若l與C交于A，B兩點(diǎn)，求

  1

  |

  OA

  |

  +

  1

  |

  OB

  |

  的值．
  組卷：151引用：2難度：0.5

  解析

[選修4-5：不等式選講]（10分）

• 23．設(shè)x,y,z為正實(shí)數(shù)，且x+y+z=4．
  （Ⅰ）證明：

  xy

  +

  xz

  ≤

  2

  2

  ；
  （Ⅱ）證明：

  （

  x

  -

  1

  ）

  2

  +

  （

  y

  -

  2

  ）

  2

  +

  （

  z

  -

  3

  ）

  2

  ≥

  4

  3

  ．
  組卷：48引用：2難度：0.7

  解析