2022-2023學年黑龍江省哈爾濱九中高二（上）開學數學試卷

一、單選（每題6分）

• 1．已知點O、A、B、C為空間不共面的四點，且向量

  a

  =

  OA

  +

  OB

  +

  OC

  ，向量

  b

  =

  OA

  +

  OB

  -

  OC

  ，則與

  a

  、

  b

  不能構成空間基底的向量是（　　）

  A． OA

  B． OB

  C． OC

  D． OA 或 OB
  組卷：591引用：10難度：0.9

  解析

• 2．若

  a

  =（2，3，m），

  b

  =（2n,6，8）且

  a

  ，

  b

  為共線向量，則m+n的值為（　　）

  A．7

  B． 5 2

  C．6

  D．8
  組卷：236引用：8難度：0.9

  解析

• 3．如圖所示，在正方體ABCD-A₁B₁C₁D₁中，棱長為a,M，N分別為A₁B和AC上的點，A₁M=AN=

  2

  a

  3

  ，則MN與平面BB₁C₁C的位置關系是（　　）

  A．相交	B．平行
  C．垂直	D．MN在平面BB1C1C內
  組卷：56引用：1難度：0.6

  解析

• 4．空間四邊形ABCD中，若向量

  AB

  =（-3，5，2），

  CD

  =（-7，-1，-4）點E，F分別為線段BC，AD的中點，則

  EF

  的坐標為（　　）

  A．（2，3，3）

  B．（-2，-3，-3）

  C．（5，-2，1）

  D．（-5，2，-1）
  組卷：1995引用：20難度：0.9

  解析

• 5．已知A（1，0，0）、B（0，1，0）、C（0，0，1），則平面ABC的一個單位法向量是（　　）

  A．（ 3 3 ， 3 3 ，- 3 3 ）	B．（ 3 3 ，- 3 3 ， 3 3 ）
  C．（- 3 3 ， 3 3 ， 3 3 ）	D．（- 3 3 ，- 3 3 ，- 3 3 ）
  組卷：217引用：9難度：0.9

  解析

四、解答題（每題14分）

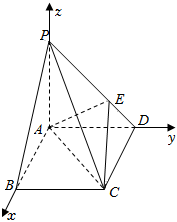• 14．如圖所示，四棱錐P-ABCD的底面是邊長為1的正方形，PA⊥CD，PA=1，PD=

  2

  ，E為PD上一點，PE=2ED．
  ①求證：PA⊥平面ABCD；
  ②在側棱PC上是否存在一點F，使得BF∥平面AEC？若存在，指出F點的位置，并證明；若不存在，說明理由．
  組卷：142引用：7難度：0.6

  解析

五、選做題（10分）

• 15．已知正方形ABCD的邊長為4，CG⊥平面ABCD，CG=2，E，F分別是AB，AD的中點，求點B到平面GEF的距離．
  組卷：14引用：1難度：0.7

  解析