2022-2023學年山東省泰安一中高一（上）期中數學試卷

一、單選題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．若集合M={-1，0，1}，N={-2，1，0}，則M∩N=（　　）

  A．{-1，0}

  B．{0，1}

  C．{0}

  D．{-1，1}
  組卷：42引用：7難度：0.9

  解析

• 2．函數

  y

  =

  x

  +

  1

  +

  1

  2

  -

  x

  的定義域為（　　）

  A．[-1，+∞）	B．[-1，2）∪（2，+∞）
  C．（-1，+∞）	D．[2，+∞）
  組卷：37引用：5難度：0.9

  解析

• 3．設lg3=a,lg5=b,則

  lg

  27

  4

  =（　　）

  A． 3 a 2 b

  B． 3 a 2 - 2 b

  C．3a-2b

  D．3a+2b-2
  組卷：784引用：4難度：0.8

  解析

• 4．“0＜x＜2”成立是“x＜2”成立的（　　）條件

  A．充分不必要	B．必要不充分
  C．充要	D．既不充分也不必要
  組卷：337引用：4難度：0.8

  解析

• 5．函數y=1-

  1

  x

  -

  1

  的圖象是（　　）

  A．

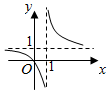
  B．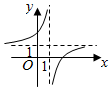

  C．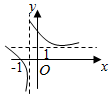

  D．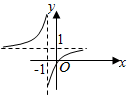
  組卷：222引用：43難度：0.9

  解析

• 6．若a、b、c為實數，則下列命題正確的是（　　）

  A．若a＞b,則ac2＞bc2	B．若a＜b＜0，則a2＞ab＞b2
  C．若a＜b,則 1 a ＞ 1 b	D．若a＜b＜0，則 b a ＞ a b
  組卷：96引用：2難度：0.7

  解析

• 7．小婷經營一花店，每天的房租水電等固定成本為100元，每束花的進價為6元．若日均銷售量Q（束）與銷售單價x（元）的關系為Q=100-5x,則當該店每天獲利最大時，每束花應定價為（　　）

  A．15元

  B．13元

  C．11元

  D．10元
  組卷：35引用：5難度：0.7

  解析

四、解答題：本題共6小題，共70分.解答應寫出必要文字說明、證明過程或演算步驟.

• 21．已知函數

  f

  （

  x

  ）

  =

  ax

  +

  b

  x

  2

  +

  4

  是定義在（-2，2）上的奇函數，且

  f

  （

  1

  2

  ）

  =

  2

  17

  ．
  （1）求函數f（x）的解析式；
  （2）用單調性定義判斷函數f（x）在區間（-2，2）上的單調性．
  組卷：48引用：4難度：0.6

  解析

• 22．黨的十八大以來，精準扶貧取得了歷史性成就，其中產業扶貧是扶貧工作的一項重要舉措，長沙某駐村扶貧小組在湘西某貧困村實施產業扶貧，計劃幫助該村進行獼猴桃的種植與銷售，為了迎合大眾需求，提高銷售量，將以裝盒售賣的方式銷售．經市場調研，若要提高銷售量，則獼猴桃的售價需要相應的降低，已知獼猴桃的種植與包裝成本為24元/盒，且每萬盒獼猴桃的銷售收入I（x）（單位：萬元）與售價量x（單位：萬盒）之間滿足關系式

  I

  （

  x

  ）

  =

  56 - 2 x , 0 ＜ x ≤ 10

  17 . 6 + 328 x - 1440 x 2 ， x ＞ 10

  ．
  （1）寫出利潤F（x）（單位：萬元）關于銷售量x（單位：萬盒）的關系式；（利潤=銷售收入-成本）
  （2）當銷售量為多少萬盒時，該村能夠獲得最大利潤？此時最大利潤是多少？
  組卷：107引用：4難度：0.6

  解析