2022年內蒙古鄂爾多斯市東勝區中考數學一模試卷

一．選擇題

• 1．如果溫度上升3℃，記作+3℃，那么溫度下降2℃記作（　　）

  A．-2℃

  B．+2℃

  C．+3℃

  D．-3℃
  組卷：4231引用：77難度：0.9

  解析

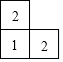• 2．如圖，是由幾個大小相同的小立方塊所搭幾何體的俯視圖，其中小正方形中的數字表示在該位置的小立方塊的個數，則這個幾何體的主視圖是（　　）

  A．

  B．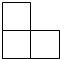

  C．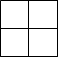

  D．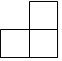
  組卷：1333引用：22難度：0.9

  解析

• 3．下列計算正確的是（　　）

  A． 4 =±2	B．（3x）-2= 1 9 x 2
  C．5a2?a3=5a6	D． （ 3 + 2 ） （ 3 - 2 ） =1
  組卷：57引用：1難度：0.7

  解析

• 4．為了解九年級學生讀書情況，隨機調查了九年級50名學生讀書的冊數．統計數據如表所示：
  

  冊數	0	1	2	3	4
  人數	1	13	16	17	3

  關于這組數據，下列說法正確的是（　　）

  A．中位數是2

  B．眾數是17

  C．平均數是2

  D．方差是20
  組卷：77引用：3難度：0.7

  解析

• 5．尺規作圖：過直線l外一點P作直線l的平行線．如圖是四位同學的作圖痕跡．其中作圖錯誤的同學是（　　）
  

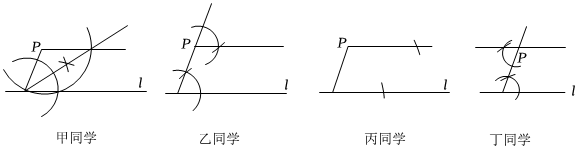
  A．甲

  B．乙

  C．丙

  D．丁
  組卷：65引用：2難度：0.6

  解析

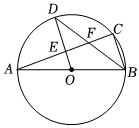• 6．如圖，AB是⊙O的直徑，C、D是⊙O上的點，且OD∥BC，AC分別與OD、BD相交于點E、F．則下列結論錯誤的是（　　）

  A．DE=BC

  B．BD平分∠ABC

  C．△DEF∽△BCF

  D．∠AOD=2∠DBC
  組卷：72引用：1難度：0.5

  解析

• 7．從東勝到鄂爾多斯站，走機場高速的全程是42千米，走東康快線的全程比機場高速的全程少6千米，但平均車速比機場高速低40%，結果所用時間比走機場高速多用12分鐘．若設走機場高速的平均速度為x千米/小時，根據題意，可列分式方程（　　）

  A． 42 - 6 （ 1 - 40 % ） x - 42 x =12	B． 42 - 6 （ 1 - 40 % ） x - 42 x = 1 5
  C． 42 x - 42 - 6 （ 1 - 40 % ） x =12	D． 42 x - 42 - 6 （ 1 - 40 % ） x = 1 5
  組卷：107引用：2難度：0.7

  解析

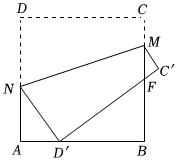• 8．如圖，將四邊形ABCD是邊長為18的正方形紙片，將其沿MN折疊，使點D落在邊AB上的D′處，點C對應點為C′，且AD′=6，則BF的長是（　　）

  A．7

  B．8

  C．9

  D．1
  組卷：130引用：1難度：0.5

  解析

三、解答題

• 24．如圖，拋物線y=-x²+bx+c與x軸交于A（3，0）、B（-1，0）兩點，與y軸交于點C，頂點為D．
  
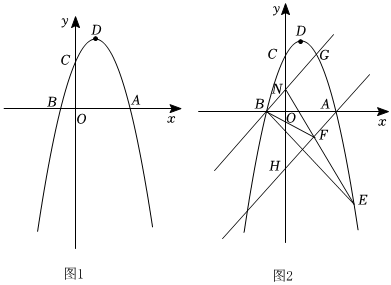
  （1）求該拋物線的解析式與頂點D的坐標．
  （2）點P是y軸上一點，點Q是拋物線上一點，是否存在以A、D、P、Q為頂點的四邊形是平行四邊形？若存在，請寫出滿足條件的點Q的坐標；若不存在，請說明理由．
  （3）若點E是第四象限拋物線上的動點，y軸上有一點N（0，1），將直線BN向下平移經過點A，連接NE交直線AH于點F，連接BE，BF．當△BEF的面積為3時，求點E的坐標．
  組卷：101引用：1難度：0.2

  解析

• 25．（1）探索發現：在幾何學習中，如果兩個三角形有公共高、公共邊，我們利用面積可以發現線段之間的一些數量關系．例如圖1，在△ABC中，點D在邊BC上，△ABD與△ADC面積分別記為S₁和S₂，若BD=2，DC=3，則S₁：S₂=

  ．
  （2）閱讀分析：如圖2，在△ABC中，AB=AC，∠BAC=90°，射線AM交BC于點D，點E、F在AM上，且∠CEM=∠BFA=90°，若△ABF的面積為5，BF：EF=1：2，求△CEF的面積．
  （3）類比探究：如圖3，在四邊形ABCD中，AB=AD，AC與BD交于點O，點E、F在射線AC上，且∠BCF=∠DEF=∠BAD．若OD=4OB，△ABC的面積為3，求出△CDE的面積．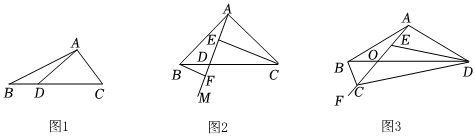
  
  組卷：309引用：1難度：0.3

  解析