2022-2023學年廣東省廣州市番禺區南雅中學九年級（上）期中數學試卷

一、選擇題（本大題共10小題，每小題3分，滿分30分.在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．如果2是方程x²-3x+k=0的一個根，則常數k的值為（　　）

  A．1

  B．2

  C．-1

  D．-2
  組卷：8114引用：95難度：0.9

  解析

• 2．如圖所示圖形中，既是軸對稱圖形，又是中心對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：20引用：1難度：0.9

  解析

• 3．如果將拋物線y=x²+2向下平移1個單位，那么所得新拋物線的表達式是（　　）

  A．y=（x-1）2+2

  B．y=（x+1）2+2

  C．y=x2+1

  D．y=x2+3
  組卷：3665引用：121難度：0.9

  解析

• 4．用配方法解方程x²+2x-1=0時，配方結果正確的是（　　）

  A．（x+1）2=2

  B．（x-1）2=2

  C．（x+2）2=3

  D．（x+1）2=3
  組卷：767引用：12難度：0.9

  解析

• 5．一元二次方程x²+2

  2

  x-6=0的兩實數根為x₁，x₂，則x₁+x₂的值為（　　）

  A． 2

  B．-2 2

  C．2 2

  D．6
  組卷：475引用：2難度：0.6

  解析

• 6．一種藥品原價每盒25元，經過兩次降價后每盒16元．設兩次降價的百分率都為x,則x滿足（　　）

  A．16（1+2x）=25	B．25（1-2x）=16
  C．16（1+x）2=25	D．25（1-x）2=16
  組卷：2928引用：40難度：0.8

  解析

• 7．設A（-2，y₁），B（1，y₂），C（2，y₃）是拋物線y=-（x+1）²+2上的三點，則y₁，y₂，y₃的大小關系為（　　）

  A．y1＞y2＞y3

  B．y1＞y3＞y2

  C．y3＞y2＞y1

  D．y3＞y1＞y2
  組卷：1453引用：23難度：0.7

  解析

• 8．如圖，△ABC中，∠CAB=65°，在同一平面內，將△ABC繞點A旋轉到△AED的位置，使得DC∥AB，則∠BAE等于（　　）

  A．30°

  B．40°

  C．50°

  D．60°
  組卷：1932引用：91難度：0.9

  解析

三、解答題（本大題共9小題，滿分72分，解答應寫出文字說明、證明過程或演算步驟）

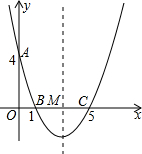• 24．如圖，在直角坐標系中，拋物線經過點A（0，4），B（1，0），C（5，0），其對稱軸與x軸相交于點M．
  （1）求拋物線的解析式和對稱軸；
  （2）在拋物線的對稱軸上是否存在一點P，使△PAB的周長最小？若存在，請求出點P的坐標；若不存在，請說明理由；
  （3）連接AC，在直線AC的下方的拋物線上，是否存在一點N，使△NAC的面積最大？若存在，請求出點N的坐標；若不存在，請說明理由．
  組卷：24293引用：123難度：0.1

  解析

• 25．如圖1，在△ABC中，點D、E分別在AB、AC上，DE∥BC，AD=AE，
  
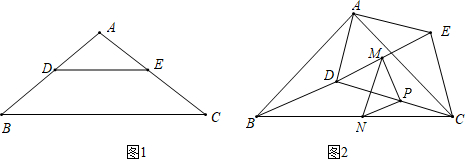
  （1）求證：∠B=∠C；
  （2）若∠BAC=90°，把△ADE繞點A逆時針旋轉到圖2的位置，點M，P，N分別為DE，DC，BC的中點，連接MN，PM，PN．
  ①判斷△PMN的形狀，并說明理由；
  ②把△ADE繞點A在平面內自由旋轉，若AD=4，AB=10，試問△PMN面積是否存在最大值；若存在，求出其最大值．若不存在，請說明理由．
  組卷：669引用：7難度：0.2

  解析