當前位置：試卷中心 > 試卷詳情

2023-2024學年海南省定安中學高二（上）開學數學試卷

發布：2024/8/9 8:0:9

1．集合A={1，2，3，4}，B={3，4，5，6}，則A∩B=（　　）
A．{1，2，3，45，6} B．{3，4} C．{1，2，3，4，5} D．{2，3，4，5，6}
組卷：29引用：1難度：0.9
解析
2．復數
2
-
i
1
-
3
i
在復平面內對應點所在的象限為（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
組卷：4717引用：19難度：0.8
解析
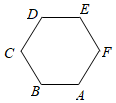3．如圖，正六邊形ABCDEF中，
BA
+
CD
+
EF
=（　　）
A．
0
B．
BE
C．
AD
D．
CF
組卷：598引用：30難度：0.9
解析
4．已知向量
a
=（2，4），
b
=（-1，1），則2
a
+
b
等于（　　）
A．（5，7） B．（5，9） C．（3，7） D．（3，9）
組卷：233引用：3難度：0.9
解析
5．已知向量
a
，
b
滿足|
a
|=1，|
b
|=
3
，|
a
-2
b
|=3，則
a
?
b
=（　　）
A．-2 B．-1 C．1 D．2
組卷：5562引用：32難度：0.7
解析
6．在△ABC中，角A，B，C的對邊分別為a,b,c,
a
=
8
3
，b=6，A=60°，則sinB=（　　）
A．
2
3
B．
6
3
C．
2
2
D．
3
8
組卷：88引用：1難度：0.9
解析
7．某市為了解高中教師對新冠肺炎防控知識的掌握情況，調研組采用分層抽樣的方法，從甲、乙、丙三所不同的高中共抽取60名教師進行調查．已知甲、乙、丙三所高中分別有180名、270名、90名教師，則從乙校中應抽取的人數為（　　）
A．10 B．20 C．30 D．40
組卷：115引用：4難度：0.9
解析

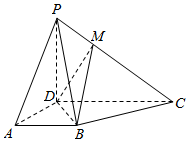21．如圖所示，已知ABCD為梯形，AB∥CD，CD=2AB．
（1）設平面PAB∩平面PDC=l,證明：AB∥l；
（2）在棱PC上是否存在點M，使得PA∥平面MBD，若存在，請確定點M的位置；若不存在，請說明理由．
組卷：999引用：6難度：0.5
解析
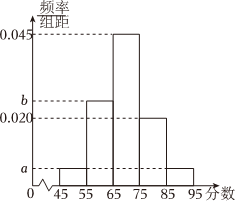22．第19屆亞運會將于2022年9月在杭州舉行，志愿者的服務工作是亞運會成功舉辦的重要保障．某高校承辦了杭州志愿者選拔的面試工作．現隨機抽取了100名候選者的面試成績，并分成五組：第一組[45，55），第二組[55，65），第三組[65，75），第四組[75，85），第五組[85，95），繪制成如圖所示的頻率分布直方圖．已知第三、四、五組的頻率之和為0.7，第一組和第五組的頻率相同．
（1）求a,b的值；
（2）根據組委會要求，本次志愿者選拔錄取率為19%，請估算被錄取至少需要多少分．
組卷：14引用：2難度：0.7
解析