2010年浙江省嘉興市桐鄉(xiāng)市九年級文理科聯(lián)賽模擬試卷（16）

一、選擇題（共10小題，每小題4分，滿分40分）

• 1．正方形ABCD中，E、F兩點(diǎn)分別是BC、CD上的點(diǎn)．若△AEF是邊長為

  2

  的等邊三角形，則正方形ABCD的邊長為（　　）

  A． 3 + 1 2

  B． 3 - 1 2

  C． 3

  D．2
  組卷：199引用：22難度：0.9

  解析

• 2．如圖，在Rt△ABC中，∠ACB=90°，AB=2BC，在直線BC或AC上取一點(diǎn)P，使得△PAB為等腰三角形，則符合條件的點(diǎn)P共有（　　）

  A．4個(gè)

  B．5個(gè)

  C．6個(gè)

  D．7個(gè)
  組卷：2733引用：40難度：0.5

  解析

• 3．如圖所示，是一塊三角形的草坪，現(xiàn)要在草坪上建一涼亭供大家休息，要使涼亭到草坪三條邊的距離相等，涼亭的位置應(yīng)選在（　　）

  A．△ABC的三條中線的交點(diǎn)

  B．△ABC三邊的中垂線的交點(diǎn)

  C．△ABC三條角平分線的交點(diǎn)

  D．△ABC三條高所在直線的交點(diǎn)
  組卷：1117引用：65難度：0.9

  解析

• 4．下列命題是真命題的是（　　）

  A．若a2=b2，則a=b	B．若x=y,則2-3x＞2-3y
  C．若x2=2，則x=± 2	D．若x3=8，則x=±2
  組卷：95引用：17難度：0.9

  解析

• 5．函數(shù)y=

  x

  +

  2

  x

  2

  -

  2

  的自變量x的取值范圍是（　　）

  A．x≥-2且x≠2

  B．x≥-2且x≠± 2

  C．x=±2

  D．全體實(shí)數(shù)
  組卷：79引用：15難度：0.9

  解析

• 6．將二次函數(shù)y=x²-2x+3化為y=（x-h）²+k的形式，結(jié)果為（　　）

  A．y=（x+1）2+4

  B．y=（x+1）2+2

  C．y=（x-1）2+4

  D．y=（x-1）2+2
  組卷：4589引用：171難度：0.9

  解析

• 7．10名同學(xué)分成甲、乙兩隊(duì)進(jìn)行籃球比賽，它們的身高（單位：cm）如下表所示：
  

  	隊(duì)員1	隊(duì)員2	隊(duì)員3	隊(duì)員4	隊(duì)員5
  甲隊(duì)	177	176	175	172	175
  乙隊(duì)	170	175	173	174	183

  設(shè)兩隊(duì)隊(duì)員身高的平均數(shù)依次為

  x

  甲

  ，

  x

  乙

  ，身高的方差依次為S_甲²，S_乙²，則下列關(guān)系中完全正確的是（　　）

  A． x 甲 = x 乙 ，S甲2＞S乙2	B． x 甲 = x 乙 ，S甲2＜S乙2
  C． x 甲 ＞ x 乙 ，S甲2＞S乙2	D． x 甲 ＜ x 乙 ，S甲2＞S乙2
  組卷：51引用：13難度：0.9

  解析

• 8．小剛用一張半徑為24cm的扇形紙板做一個(gè)如圖所示的圓錐形小丑帽子側(cè)面（接縫忽略不計(jì)），如果做成的圓錐形小丑帽子的底面半徑為10cm,那么這張扇形紙板的面積是（　　）

  A．120πcm2

  B．240πcm2

  C．260πcm2

  D．480πcm2
  組卷：431引用：42難度：0.9

  解析

三、解答題（共5小題，滿分37分）

• 24．已知一次函數(shù)y₁=ax+b的圖象與反比例函數(shù)y₂=

  k

  x

  的圖象相交于A、B兩點(diǎn)，坐標(biāo)分別為（-2，4）、（4，-2）．
  （1）求兩個(gè)函數(shù)的解析式；
  （2）結(jié)合圖象寫出y₁＜y₂時(shí)，x的取值范圍；
  （3）求△AOB的面積；
  （4）是否存在一點(diǎn)P，使以點(diǎn)A、B、O、P為頂點(diǎn)的四邊形為菱形？若存在，求出頂點(diǎn)P的坐標(biāo)；若不存在，請說明理由．
  組卷：517引用：19難度：0.1

  解析

• 25．如圖，OABC是一張放在平面直角坐標(biāo)系中的矩形紙片，O為原點(diǎn)，點(diǎn)A在x軸的正半軸上，點(diǎn)C在y軸的正半軸上，OA=5，OC=3．
  （1）在AB邊上取一點(diǎn)D，將紙片沿OD翻折，使點(diǎn)A落在BC邊上的點(diǎn)E處，求點(diǎn)D，E的坐標(biāo)；
  （2）若過點(diǎn)D，E的拋物線與x軸相交于點(diǎn)F（-5，0），求拋物線的解析式和對稱軸方程；
  （3）若（2）中的拋物線與y軸交于點(diǎn)H，在拋物線上是否存在點(diǎn)P，使△PFH的內(nèi)心在坐標(biāo)軸上？若存在，求出點(diǎn)P的坐標(biāo)，若不存在，請說明理由．
  （4）若（2）中的拋物線與y軸相交于點(diǎn)H，點(diǎn)Q在線段OD上移動(dòng)，作直線HQ，當(dāng)點(diǎn)Q移動(dòng)到什么位置時(shí)，O，D兩點(diǎn)到直線HQ的距離之和最大？請直接寫出此時(shí)點(diǎn)Q的坐標(biāo)及直線HQ的解析式．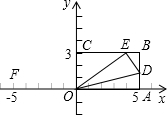
  
  組卷：216引用：29難度：0.1

  解析