2023-2024學年重慶市西南大學附中高三（上）期中數學試卷

一、單項選擇題：本大題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．集合

  A

  =

  {

  x

  |

  y

  =

  -

  x

  2

  +

  2

  x

  +

  3

  }

  ，集合B={y|y=e^x}，則A∪B=（　　）

  A．（0，1]

  B．（0，3]

  C．[-1，+∞）

  D．[-3，+∞）
  組卷：209引用：5難度：0.8

  解析

• 2．已知扇形的圓心角是60°，半徑為2，則扇形的面積為（　　）

  A．60

  B．120

  C． π 3

  D． 2 π 3
  組卷：287引用：1難度：0.8

  解析

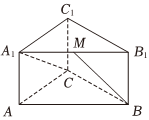• 3．如圖，正三棱柱ABC-A₁B₁C₁中，AB=2AA₁，M是A₁B₁的中點，則異面直線A₁C與BM所成角的余弦值為（　　）
  ?

  A． 6 2

  B． 10 5

  C． 6 3

  D． 15 5
  組卷：93引用：3難度：0.6

  解析

• 4．“tanx=tany”是“x=y+2kπ（k∈Z）”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：205引用：5難度：0.5

  解析

• 5．若a＞0，b＞0，a+b=4，則下列結論正確的是（　　）

  A． a + b ≤ 2	B．2a+2b≥8
  C．（a+1）2+（b+3）2≤32	D． a 2 3 + b 2 ≥ 6
  組卷：71引用：1難度：0.5

  解析

• 6．正四棱錐P-ABCD的高為3，體積為32，則其外接球的表面積為（　　）

  A． 625 36 π

  B． 625 18 π

  C． 625 9 π

  D． 25 6 π
  組卷：131引用：1難度：0.7

  解析

• 7．一個蛋糕店制作一個大型蛋糕，蛋糕是由多個高度均為0.1米的圓柱形蛋糕重疊而成，上層蛋糕會覆蓋相鄰下層蛋糕的上底面一半的面積，最底層蛋糕的半徑為1米．若該蛋糕的體積至少為0.6立方米，則蛋糕至少需要做的層數為（　　）（其中 π≈3.14）

  A．3

  B．4

  C．5

  D．6
  組卷：9引用：1難度：0.6

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

• 21．王老師每天早上7：00準時從家里出發去學校，他每天只會從地鐵與汽車這兩種交通工具之間選擇一個乘坐．王老師多年積累的數據表明，他到達學校的時間在兩種交通工具下的概率分布如下表所示：
  

  到校時間	7：30之前	7：30-7：35	7：35-7：40	7：40-7：45	7：45-7：50	7：50之后
  乘地鐵	0.1	0.15	0.35	0.2	0.15	0.05
  乘汽車	0.25	0.3	0.2	0.1	0.1	0.05

  （例如：表格中0.35的含義是如果王老師當天乘地鐵去學校，則他到校時間在7：35-7：40的概率為0.35．）
  （1）某天早上王老師通過拋一枚質地均勻的硬幣決定乘坐地鐵還是乘坐汽車去學校，若正面向上則坐地鐵，反面向上則坐汽車．求他當天7：40-7：45到校的概率；
  （2）已知今天（第一天）王老師選擇乘坐地鐵去學校，從第二天開始，若前一天到校時間早于7：40，則當天他會乘坐地鐵去學校，否則當天他將乘坐汽車去學校．且若他連續10天乘坐地鐵，則不論他前一天到校的時間是否早于7：40，第11天他都將坐汽車到校．記他從今天起（包括今天）到第一次乘坐汽車去學校前坐地鐵的次數為X，求E（X）；
  （3）已知今天（第一天）王老師選擇乘坐地鐵去學校．從第二天開始，若他前一天坐地鐵去學校且到校時間早于7：40，則當天他會乘坐地鐵去學校；若他前一天坐地鐵去學校且到校時間晚于7：40，則當天他會乘坐汽車去學校；若他前一天乘坐汽車去學校，則不論他前一天到校的時間是否早于7：40，當天他都會乘坐地鐵去學校．記P_n為王老師第n天坐地鐵去學校的概率，求{P_n}的通項公式．
  組卷：128引用：2難度：0.5

  解析

• 22．已知f（x）=2ae^1-x（1-x），其中a≠0．
  （1）求f（x）在 x=1 處的切線方程；
  （2）若f（x）+

  1

  a

  x³-x≥0在[

  1

  2

  ，+∞）上恒成立，求a的取值范圍．
  組卷：68引用：1難度：0.1

  解析