2022-2023學年廣東省韶關市高二（下）期末數學試卷

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．設全集U={1，2，4，5，7，8}，集合A={1，2，5}，集合B={2，7，8}，則?_U（A∪B）=（　　）

  A．4	B．（1，2，5，7，8）
  C．{4}	D．{2}
  組卷：115引用：3難度：0.9

  解析

• 2．在復平面內，復數1-2i與-1+3i分別對應向量

  ON

  和

  OM

  ，其中O為坐標原點，則

  |

  NM

  |

  =（　　）

  A．1

  B．5

  C． 2

  D． 29
  組卷：19引用：2難度：0.8

  解析

• 3．已知

  a

  =

  lo

  g

  1

  2

  1

  3

  ，

  b

  =

  （

  1

  3

  ）

  1

  2

  ，c=cosπ，則（　　）

  A．a＞b＞c

  B．b＞a＞c

  C．c＞b＞a

  D．a＞c＞b
  組卷：31引用：2難度：0.7

  解析

• 4．已知α，β是空間中兩個不同的平面，m,n是空間中兩條不同的直線，則（　　）

  A．若m∥α，n∥α，則m∥n	B．若m∥α，m∥β，則α∥β
  C．若α⊥β，m?α，則m⊥β	D．若m⊥α，n⊥β，m⊥n,則α⊥β
  組卷：63引用：3難度：0.7

  解析

• 5．

  f

  （

  x

  ）

  =

  （

  1

  -

  e

  x

  1

  +

  e

  x

  ）

  ?

  cos

  （

  3

  2

  π

  +

  x

  ）

  部分圖象大致是（　　）

  A．	B．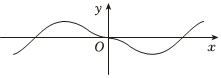
  C．	D．
  組卷：43引用：4難度：0.6

  解析

• 6．已知向量

  a

  =

  （

  3

  ，

  1

  ）

  ，

  b

  =

  （

  1

  ，

  1

  ）

  ，則向量

  a

  在向量

  b

  上的投影向量為（　　）

  A． （ 3 + 1 2 ， 1 ）	B． （ 3 + 1 2 ， 3 + 1 2 ）
  C． （ 3 - 1 2 ， 3 - 1 2 ）	D． （ 1 ， 3 - 1 2 ）
  組卷：29引用：2難度：0.8

  解析

• 7．已知點F₁，F₂是雙曲線

  C

  ：

  x

  2

  -

  y

  2

  3

  =

  1

  的左、右焦點，點P是雙曲線C右支上一點，過點F₂向∠F₁PF₂的角平分線作垂線，垂足為點Q，則點

  A

  （

  -

  3

  ，

  1

  ）

  和點Q距離的最大值為（　　）

  A．2

  B． 7

  C．3

  D．4
  組卷：73引用：3難度：0.4

  解析

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

• 21．已知函數f（x）=lnx-x,

  h

  （

  x

  ）

  =

  a

  e

  x

  x

  +

  1

  ，a∈R．
  （1）求曲線y=f（x）過坐標原點的切線方程；
  （2）若f（x）+h（x）≥0在[1，+∞）恒成立，求a的取值范圍．
  組卷：63引用：2難度：0.5

  解析

• 22．已知橢圓

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的離心率是

  1

  2

  ，且過點

  M

  （

  1

  ，

  3

  2

  ）

  ．
  （1）求橢圓C的方程；
  （2）橢圓C的左、右頂點分別為A₁，A₂，且P，Q為橢圓C上異于A₁，A₂的點，若直線PQ過點

  （

  1

  2

  ，

  0

  ）

  ，是否存在實數λ，使得

  k

  A

  1

  P

  =

  λ

  k

  A

  2

  Q

  恒成立．若存在，求實數λ的值；若不存在，說明理由．
  組卷：46引用：2難度：0.5

  解析