當前位置：試卷中心 > 試卷詳情

2022-2023學年江蘇省揚州市江都二中九年級（上）期末數學試卷

發布：2024/12/4 11:30:1

一、選擇題（本大題共8小題，每小題3分，共24分．在每小題所給出的四個選項中，只有一項是符合題目要求的，請將正確選項的序號填涂在答題卡相應位置上）

1．方程x²=4的解是（　　）
A．x₁=x₂=2 B．x₁=x₂=-2 C．x₁=2，x₂=-2 D．x₁=4，x₂=-4
組卷：102引用：3難度：0.6
解析
2．已知⊙O的半徑是4，OP=3，則點P與⊙O的位置關系是（　　）
A．點P在圓上 B．點P在圓內 C．點P在圓外 D．不能確定
組卷：200引用：13難度：0.9
解析
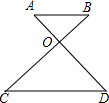3．如圖，已知AB∥CD，下列式子錯誤的是（　　）
A．
AB
OB
=
CD
OC
B．
AB
OA
=
CD
OD
C．
OB
OC
=
AD
OD
D．
OA
OD
=
OB
OC
組卷：65引用：1難度：0.5
解析
4．下列說法正確的是（　　）
A．等弧所對的圓周角相等
B．平分弦的直徑垂直于弦
C．相等的圓心角所對的弧相等
D．圓是軸對稱圖形，任何一條直徑都是它的對稱軸
組卷：238引用：6難度：0.6
解析
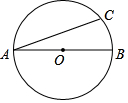5．如圖，AB是⊙O的直徑，
?
AC
=
3
?
BC
，則∠BAC的度數為（　　）
A．22.5° B．30° C．45° D．67.5°
組卷：496引用：5難度：0.7
解析
6．如圖，a＜0，b＞0，c＜0，那么二次函數y=ax²+bx+c的圖象可能是（　　）
A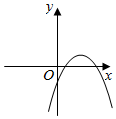． B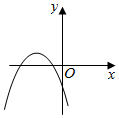． C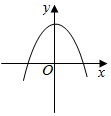． D．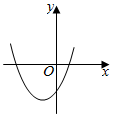
組卷：298引用：7難度：0.5
解析
7．關于x的一元二次方程ax²+2x-1=0有兩個不相等實數根，則整數a最小是（　　）
A．-1 B．0 C．1 D．2
組卷：174引用：1難度：0.6
解析
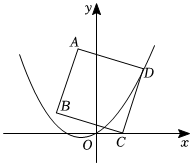8．如圖，在正方形ABCD中，點A、C的坐標分別是（-1，4），（1，0），點D在拋物線
y
=
1
2
x
2
+
mx
的圖象上，則m的值是（　　）
A．
2
3
B．
1
2
C．
7
3
D．1
組卷：465引用：2難度：0.5
解析

二、填空題（共10小題，每小題3分，滿分30分）

9．
b
a
=
3
2
，
a
+
b
a
=

．
組卷：110引用：4難度：0.9
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（本大題共10小題，共96分，請在答題卡指定區域內作答，解答時應寫出文字說明、證明過程或演算步驟．）

27．已知拋物線y=-x²+bx+c與x軸交于A、B兩點（點A在點B的左側），與y軸的交點為C（0，3），其對稱軸是直線x=1，點P是拋物線上第一象限內的點，過點P作PQ⊥x軸，垂足為Q，交BC于點D，且點P的橫坐標為a.
（1）求這條拋物線對應的函數表達式；
（2）如圖1，過點C作CE平行于x軸，交拋物線于點E，若點P在CE的上方，連接PE，PC，DE，當S_{四邊形CPED}=
4
3
S_△AOC時，求點P坐標；
（3）如圖2，連接AP，BP，設AP交BC于點H，△PHB的面積為S₁，△ABH的面積為S₂，求
S
1
S
2
的最大值；
（4）如圖3，在（3）的條件下，連接CQ，將CQ右側的拋物線沿CQ翻折，交y軸于點M，請直接寫出點M的坐標．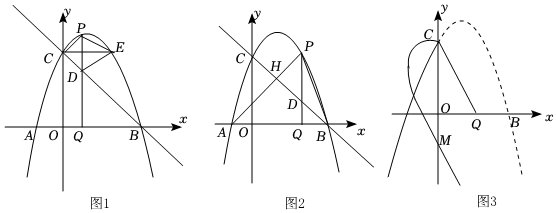
組卷：854引用：2難度：0.2
解析
28．在平面直角坐標系xOy中，圖形W上任意兩點間的距離若有最大值，將這個最大值記為d.對于點P和圖形W給出如下定義：點Q是圖形W上任意一點，若P，Q兩點間的距離有最小值，且最小值恰好為d,則稱點P為圖形W的“關聯點”．

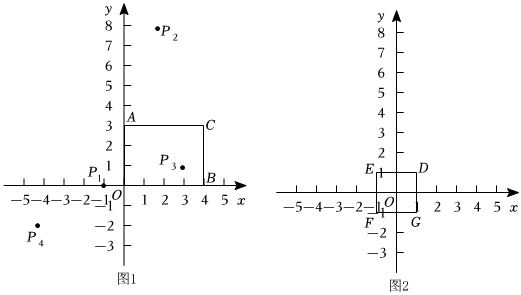
（1）如圖1，圖形W是矩形AOBC，其中點A的坐標為（0，3），點C的坐標為（4，3），則d=
．在點P₁（-1，0），P₂（2，8），P₃（3，1），
P
4
（
-
21
，-
2
）
中，矩形AOBC，的“關聯點”是
；
（2）如圖2，圖形W是中心在原點的正方形DEFG，其中D點的坐標為（1，1）．若直線y=x+b上存在點P，使點P為正方形DEFG的“關聯點”，求b的取值范圍；
（3）已知點M（1，0），
N
（
0
，
3
）
．圖形W是以T（t,0）為圓心，1為半徑的?T，若線段MN上存在點P，使點P為?T的“關聯點”，直接寫出t的取值范圍．
組卷：271引用：2難度：0.4
解析