2022-2023學年北京六十六中高二（上）期中數學試卷

一、選擇題（每小題5分，共50分）

• 1．在空間直角坐標系中，已知M（-1，0，2），N（3，2，-4），則MN的中點P到坐標原點O的距離為（　　）

  A． 3

  B． 2

  C．2

  D．3
  組卷：92引用：2難度：0.8

  解析

• 2．若兩條直線l₁：x+2y-6=0與l₂：x+ay-7=0平行，則a的值為（　　）

  A．-2

  B． - 1 2

  C． 1 2

  D．2
  組卷：10引用：2難度：0.8

  解析

• 3．已知向量

  a

  =（-1，2，1），

  b

  =（3，x,y），且

  a

  ∥

  b

  ，那么|

  b

  |=（　　）

  A． 3 6

  B．6

  C．9

  D．18
  組卷：431引用：24難度：0.8

  解析

• 4．如圖，在平行六面體ABCD-A₁B₁C₁D₁中，若

  B

  D

  1

  =x

  AB

  +y

  AD

  +z

  A

  A

  1

  ，則（x,y,z）=（　　）

  A．（-1，1，1）

  B．（1，-1，1）

  C．（1，1，-1）

  D．（-1，-1，-1）
  組卷：590引用：13難度：0.8

  解析

• 5．已知空間中兩條不同的直線m,n,一個平面α，則“直線m,n與平面α所成角相等”是“直線m,n平行”的（　　）

  A．充分而不必要條件	B．必要而不充分條件
  C．充分必要條件	D．既不充分也不必要
  組卷：24引用：2難度：0.7

  解析

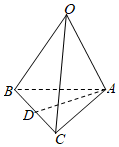• 6．如圖，在三棱錐O-ABC中，D是BC的中點，若

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，則

  AD

  等于（　　）

  A．- a + b + c

  B．- a + b - c

  C．- a + 1 2 b + 1 2 c

  D． - a - 1 2 b - 1 2 c
  組卷：634引用：10難度：0.7

  解析

• 7．已知點M（a,b）在圓O：x²+y²=1外，則直線ax+by=1與圓O的位置關系是（　　）

  A．相交

  B．相切

  C．相離

  D．不確定
  組卷：355引用：11難度：0.7

  解析

三、解答題（本題共5小題，共70分）

• 20．如圖，在四棱柱ABCD-A₁B₁C₁D₁中，AA₁⊥平面ABCD，底面ABCD滿足AD∥BC且AB=AD=AA₁=2，BD=DC=2

  2

  ．
  （1）求證：AB⊥平面ADD₁A₁；
  （2）求直線AB與平面B₁CD₁所成角的正弦值；
  （3）求點C₁到平面B₁CD₁的距離．
  組卷：88引用：3難度：0.5

  解析

• 21．如圖1，矩形ABCD，AB=1，BC=2，點E為AD的中點，將△ABE沿直線BE折起至平面PBE⊥平面BCDE（如圖2），點M在線段PD上，PB∥平面CEM．
  （1）求證：MP=2DM；
  （2）求二面角B-PE-C的大小；
  （3）若在棱PB，PE分別取中點F，G，試判斷點M與平面CFG的關系，并說明理由．
  組卷：85引用：3難度：0.5

  解析