2023-2024學年福建省龍巖市一級校聯盟高一（上）期中數學試卷

一、單項選擇題：本大題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一頁符合題目要求.

• 1．已知集合M={-1，0，1，2，3}，N={x|-1≤x＜3}，則M∩N=（　　）

  A．{0，1，2}

  B．{-1，0，1}

  C．M

  D．{-1，0，1，2}
  組卷：116引用：7難度：0.8

  解析

• 2．函數

  f

  （

  x

  ）

  =

  （

  x

  -

  1

  ）

  0

  +

  1

  x

  的定義域是（　　）

  A．（1，+∞）	B．（0，+∞）
  C．（0，2）∪（2，+∞）	D．（0，1）∪（1，+∞）
  組卷：69引用：1難度：0.9

  解析

• 3．已知函數

  f

  （

  x

  ）

  =

  2 x + 1 ， x ＜ 2 ，

  f （ x - 3 ） ， x ≥ 2 ，

  則f（6）=（　　）

  A．65

  B．9

  C．2

  D．1
  組卷：9引用：1難度：0.8

  解析

• 4．下列函數中，是偶函數且在區間（0，+∞）上單調遞增的是（　　）

  A．f（x）=|x-1|

  B．f（x）=x2-1

  C． f （ x ） = x 2 - 1 x

  D． f （ x ） = （ 1 2 ） | x |
  組卷：19引用：1難度：0.7

  解析

• 5．已知x∈R，則“x²＞1“是“x＞1”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：106引用：6難度：0.7

  解析

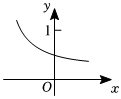• 6．若f（x）=a^x-b的圖像如圖，（a,b是常數），則（　　）

  A．a＞1，b＜0

  B．a＞1，b＞0

  C．0＜a＜1，b＞0

  D．0＜a＜1，b＜0
  組卷：511引用：3難度：0.7

  解析

• 7．設a=0.3^0.6，b=0.6^0.3，c=1.1^0.1，則（　　）

  A．c＞b＞a

  B．c＞a＞b

  C．a＞c＞b

  D．b＞a＞c
  組卷：142引用：1難度：0.7

  解析

四、解答題：本大題共6小題，共70分.解答應寫出必要的文字說明、證明過程或演算步驟.

• 21．2023年6月5日是第50個世界環境日，口號是“減塑撿塑”．中國的主題是“建設人與自然和諧共生的現代化”．世界環境日的意義在于提醒全世界注意地球狀況和人類活動對環境的危害．某企業生產某種環保型產品的年固定成本為1200萬元，每生產x（百件），需另投入成本C（x）（萬元）．經調研測算，若年產量x（百件）低于100（百件），則這x（百件）產品成本

  C

  （

  x

  ）

  =

  1

  3

  x

  2

  +

  30

  x

  +

  450

  ；若年產量x（百件）不低于100（百件）時，則這x（百件）產品成本

  C

  （

  x

  ）

  =

  110

  x

  +

  8000

  x

  -

  90

  -

  4900

  ．每百件產品售價為90萬元，設該企業生產的產品能全部售完．
  （1）寫出年利潤L（x）（萬元）關于年產量x（百件）的函數解析式．
  （2）當年產量為多少百件時，企業所獲利潤最大？最大利潤是多少？
  組卷：9引用：1難度：0.6

  解析

• 22．已知函數g（x）=ax²-2ax+b+1（a＞0）在區間[0，3]上有最大值4和最小值0，設函數

  f

  （

  x

  ）

  =

  g

  （

  x

  ）

  x

  ．
  （1）求a,b的值．
  （2）設函數h（x）=f（9^x）+mf（3^x）+2m+2，是否存在實數m,使得h（x）在區間（0，+∞）上存在最小值？若存在，求出實數m的取值范圍，若不存在，請說明理由．
  組卷：11引用：1難度：0.7

  解析