2022年江蘇省南京市寧海中學高考數(shù)學模擬試卷（4月份）

一、選擇題（本大題共8小題，每小題5分，共40分．在每小題中，只有一項是符合題目要求的）

• 1．設集合A={x|

  x

  +

  1

  x

  -

  4

  ≤0}，B={y|y=1-e^x，x∈R}，R為實數(shù)集，則?_R（A∪B）=（　　）

  A．{x|x＜-1或x≥1}

  B．{x|x≤-1或x＞1}

  C．{x|x≥4}

  D．{x|x＞4}
  組卷：95引用：2難度：0.8

  解析

• 2．若復數(shù)（1-i）（a+i）在復平面內對應的點在第二象限，則實數(shù)a的取值范圍是（　　）

  A．（-∞，1）

  B．（-∞，-1）

  C．（1，+∞）

  D．（-1，+∞）
  組卷：5218引用：39難度：0.9

  解析

• 3．若命題“?x∈[1，4]時，x²＞m”是假命題，則m的取值范圍（　　）

  A．m≥16

  B．m≥1

  C．m＜16

  D．m＜1
  組卷：76引用：1難度：0.7

  解析

• 4．已知在10件產品中可能存在次品，從中抽取2件檢查，記次品數(shù)為X，已知

  P

  （

  X

  =

  1

  ）

  =

  16

  45

  ，且該產品的次品率不超過30%，則這10件產品中次品數(shù)n為（　　）

  A．1件

  B．2件

  C．8件

  D．2件或8件
  組卷：117引用：2難度：0.7

  解析

• 5．函數(shù)f（x）=

  ln

  （

  x

  2

  -

  4

  x

  +

  4

  ）

  （

  x

  -

  2

  ）

  5

  的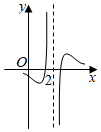圖象大致為（　　）

  A．

  B．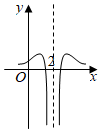

  C．

  D．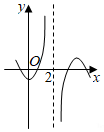
  組卷：267引用：4難度：0.9

  解析

• 6．將函數(shù)f（x）=4sin（2x+

  π

  4

  ）的圖象向右平移φ個單位，再將圖象上每一點的橫坐標縮短到原來的

  1

  2

  ，所得圖象關于直線x=

  π

  4

  對稱，則φ的最小正值為（　　）

  A． π 8

  B． 3 π 8

  C． 3 π 4

  D． π 2
  組卷：181引用：6難度：0.7

  解析

• 7．已知△ABC中，

  BD

  =

  1

  3

  BC

  ，

  AE

  =

  1

  2

  AC

  ，AD與BE交于點P，且

  AP

  =

  λ

  AD

  ，

  BP

  =

  μ

  BE

  ，則

  λ

  μ

  =（　　）

  A． 2 3

  B． 3 2

  C． 4 3

  D． 3 4
  組卷：202引用：2難度：0.7

  解析

四、解答題（本大題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟）

• 21．已知平面上一動點P到定點F（1，0）的距離與它到定直線x=-1的距離相等，設動點P的軌跡為曲線C．
  （1）求曲線C的軌跡方程；
  （2）已知點B（2，

  2

  2

  ），過點B引圓M：（x-4）²+y²=r²（0＜r＜2）的兩條切線BP，BQ，切線BP、BQ與曲線C的另一交點分別為P、Q，線段PQ中點N的縱坐標記為λ，求λ的取值范圍．
  組卷：65引用：2難度：0.5

  解析

• 22．已知函數(shù)f（x）=e^x，g（x）=lnx,a∈R．
  （1）設h（x）=g（x）-ax²，討論函數(shù)h（x）的單調區(qū)間；
  （2）求證：對任意正數(shù)a,總存在正數(shù)x,使得不等式

  |

  f

  （

  x

  ）

  -

  1

  x

  -

  1

  |

  ＜

  a

  成立．
  組卷：93引用：1難度：0.5

  解析